পরিচয় সঙ্কট: বোসন এবং ফার্মিয়ন

সৌরজগতের গ্রহদের মতোই আণুবীক্ষণিক কণাদের ঘূর্ণন-ভরবেগ (Angular momentum) রয়েছে। কণাদের এই ঘূর্ণন-ভরবেগকে বলে স্পিন (Spin)। গ্রহদের যেমন ঘূর্ণন অক্ষ থাকে, তেমনি কণাদেরও ঘূর্ণন অক্ষ আছে। স্পিন কণাদের একটি সহজাত বৈশিষ্ট্য (Intrinsic property)। চার্জ কিংবা ভরের মতোই প্রতিটি কণা জন্মের সময় এই স্পিন বৈশিষ্ট্যটি পেয়ে থাকে। কণাদের এই স্পিন বৈশিষ্ট্যের প্রমাণ পাওয়া যায় স্টার্ন-গেরল্যাখ যন্ত্রের (Stern-Gerlach apparatus) মাধ্যমে।

স্টার্ন-গেরল্যাখ যন্ত্রে একটি অসম চুম্বকক্ষেত্র তৈরি করা হয়, যন্ত্রের একদিকে চুম্বকক্ষেত্র প্রবল অন্যদিকে দুর্বল। কণারা এই চুম্বকক্ষেত্রের একদিক দিয়ে ঢোকে এবং অসম চুম্বকক্ষেত্রের প্রভাবে ভিন্ন ভিন্ন স্পিনযুক্ত কণারা ভিন্ন ভিন্নভাবে বিক্ষিপ্ত হয়ে যন্ত্রের অন্যদিক দিয়ে বেরিয়ে যায়। অর্থাৎ, স্টার্ন-গেরল্যাখ যন্ত্র থেকে বেরিয়ে যাওয়া কণাদের গতিপথের এই বিচ্যুতি পুরোপুরি নির্ভর করে কণাদের স্পিনের ওপর।

কণাদের স্পিন নির্ণয়ের জন্য আমাদেরকে ত্রিমাত্রিক কার্টেসিয়ান স্থানাঙ্কের সাহায্য নিতে হবে। গ্রহজগতের ঘূর্ণন-ভরবেগ যেকোন নিরবচ্ছিন্ন মান নিতে পারে। এবং একটি গ্রহের ঘূর্ণন-ভরবেগের X, Y, এবং Z উপাংশের (Component) প্রতিটিকে নিখুঁতভাবে নির্ণয় করা সম্ভব। যেমন: পৃথিবী এবং সূর্য যেই কাল্পনিক সমতলে অবস্থান করে তাকে বলে এলিপ্টিক-সমতল (Ecliptic plane)। পৃথিবীর ঘূর্ণন অক্ষ এই এলিপ্টিক সমতলের সাথে 66.3° কোণ করে থাকে। কিন্তু, কণাদের ক্ষেত্রে এই দুইটি বিষয় সত্য নয়। প্রথমত, কণাদের স্পিন পাওয়া যায় বিচ্ছিন্ন বা কোয়ান্টা আকারে। স্পিনের একক ħ, এখানে ħ = h/2π। যেমন: ইলেক্ট্রনের স্পিন হতে পারে +1/2ħ বা -1/2ħ। স্পিন (+) পজিটিভ বা ধনাত্মক কিংবা (-) নেগেটিভ বা ঋণাত্মক হতে পারে। আমাদের মহাবিশ্বে সবচেয়ে গুরুত্বপূর্ণ স্পিন সংখ্যাটি হলো 1/2। যেই কণারা পদার্থ তৈরি করে যেমন: ইলেক্ট্রন, প্রোটন, ও নিউট্রন এরা সবাই 1/2-স্পিন কণা। দ্বিতীয়ত, ত্রিমাত্রিক স্থানাঙ্কে স্পিনের যেকোনো একটি অক্ষের উপাংশ (X, বা Y, বা Z) নির্ণয় করা যায়, হেইজেনবার্গের অনিশ্চয়তার-নীতির কারণে একাধিক অক্ষের উপাংশ নির্ণয় করা যায় না। সুবিধার জন্য আমরা এখানে শুধুই X এবং Z-অক্ষ নিয়ে আলোচনা করবো। Y-অক্ষ নিয়ে কাজ করলে কোয়ান্টাম-স্টেটের এম্প্লিটিউড জটিল-সংখ্যায় (Complex number) চলে আসবে, তাই Y-অক্ষ এড়িয়ে যাওয়া হলো। আমরা ধরে নেবো, স্পিনের Y-উপাংশ শূন্য।

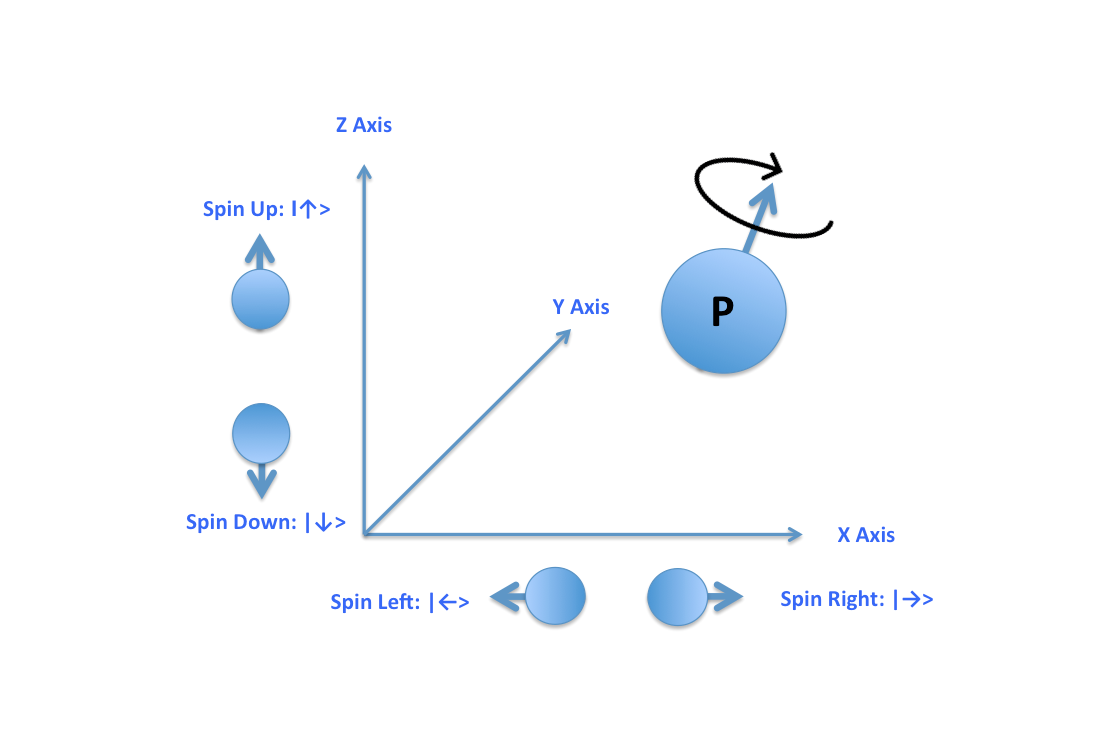
স্পিনের Z-উপাংশটি যদি উপরদিকে লম্ব হয় তবে স্টেট হবে ।↟>; এর মান +1/2। কিন্তু, Z-উপাংশটি যদি নিচের দিক বরাবর লম্ব হয় তবে স্টেট হবে ।↡>, এর মান -1/2।  একইভাবে, X-উপাংশটির ডান দিকের স্টেট ।↠>, এর মান +1/2। এবং X-উপাংশটির বাঁয়ের স্টেট ।↞>, এর মান -1/2। বোঝাই যাচ্ছে, স্পিন পরিমাপের ক্ষেত্রে স্থানাঙ্কের যেকোনো একটি অক্ষ, X বা Z ব্যবহার করাই যথেষ্ট। গুরুত্বপূর্ণ ব্যাপার হলো, একটি অক্ষের উপাংশকে  অন্য অক্ষের উপাংশগুলোর সুপারপজিশন-স্টেট আকারে প্রকাশ করা যায়। যেমন: স্পিনের X-উপাংশের বেসিস-স্টেটগুলো হলো, ।↠> এবং ।↞>; এদের সুপারপজিশন-স্টেটগুলো হলো:

।↠> = s।↟> + s।↡>;
।↞> = s।↟> – s।↡>;

Z-উপাংশের বেসিস-স্টেটগুলো, ।↟> এবং ।↡>; এদের সুপারপজিশন-স্টেটগুলো হলো:

।↟> =s।↠> + s।↞>;
।↡> =s।↠> – s।↞>;

এখানে, s^2 = 1/2।

যদি Z-অক্ষ বরাবর স্পিন পরিমাপ করতে হয়, তবে স্টার্ন-গেরল্যাখ যন্ত্রকে Z-অক্ষ বরাবর স্থাপন করতে হবে। অথবা, যদি X-অক্ষ বরাবর পরিমাপ করতে হয় তবে স্টার্ন-গেরল্যাখ যন্ত্রকে X-অক্ষ বরাবর স্থাপন করতে হবে। ওপারে সম্পর্ক থেকে বোঝাই যাচ্ছে, আমরা যদি X-উপাংশ নির্ণয় করি তবে প্রতিটি Z-উপাংশের সম্ভাবনা ৫০%। অন্যদিকে, Z-উপাংশ নিশ্চিতভাবে নির্ণয় করতে পুরো স্টার্ন-গেরল্যাখ যন্ত্রকে Z-অক্ষ বরাবর ঘোরাতে হবে। অর্থাৎ, Z এবং X-উপাংশের পরিমাপ দুটি আলাদা আলাদা এক্সপেরিমেন্ট। বলা যায়, স্পিনের X-উপাংশ এবং Z-উপাংশ পরস্পরের পরিপূরক। এরা কম্প্লিমেন্টারিটি-প্রিন্সিপল অনুসরণ করে, ফলে এদের ক্ষেত্রে হেইজেনবার্গের অনিশ্চয়তার-নীতি প্রযোজ্য। এর মানে হলো, আমরা যদি X-উপাংশ নির্ণয় করি তবে Z-উপাংশ  নির্ণয় করতে পারবো না। কিংবা,  Z-উপাংশ নির্ণয় করলে X-উপাংশ অনির্ণেয় থেকে যাবে। তাই, আগে থেকেই আমাদের সিদ্ধান্ত নিতে হবে, আমরা কোন এক্সপেরিমেন্ট চালাবো, X-উপাংশের নাকি Z-উপাংশের।

বাস্তবে কোনো কণার স্পিন পুরোপুরি Z কিংবা X-অক্ষ বরাবর না হবারই কথা। এখন কোনো কণার স্পিন যদি Z-অক্ষের সাথে α° কোণ করে থাকে, এবং আমরা যদি Z-উপাংশের এক্সপেরিমেন্ট চালাই, তবে ঐ কণার স্পিন +1/2 কণা হবার সম্ভাবনা কতো? প্রথমে আমরা স্টার্ন-গেরল্যাখ যন্ত্র Z-অক্ষ বরাবর স্থাপন করবো। এরপর যদি আমরা ঐ কণাকে এই যন্ত্রের ভেতর দিয়ে যেতে দেই, তবে α-এর বিভ্ন্নি মানের জন্য কণাটির স্পিন +1/2 হওয়ার সম্ভাবনার নিচের তালিকা থেকে পাওয়া যাবে।

ওপরে ছবি অনুসারে, যখন, α = 0°; তখন কণার স্টেট ।0°> = ।↟>; অর্থাৎ কণার স্পিন উপরের দিকে ফলে Z-উপাংশের পরিমাপ সবসময়ই +1/2 হবে, যার সম্ভাবনা 1.00 দেখানো হয়েছে। যখন, α = 180°; তখন কণার স্টেট ।180°> = ।↡>; অর্থাৎ, কণার স্পিন নিচের দিকে, তাই  Z-উপাংশের পরিমাপ সবসময়ই -1/2 হবে, ফলে স্পিন +1/2 হবার কোনোই সম্ভাবনা নেই, যার সম্ভাবনা 0.00 দেখানো হয়েছে। যখন, α = 90°; তখন কণার স্টেট ।90°> = ।↠>; অর্থাৎ কণার স্পিন ডান দিকে, ফলে Z-উপাংশের পরিমাপ +1/2 হবার সম্ভাবনা 50%। একইভাবে যখন α = 45° এবং 135°; কণার স্টেট যথাক্রমে ।45°> এবং ।135°>; Z-উপাংশের পরিমাপ +1/2 হবার সম্ভাবনা যথাক্রমে 85% এবং 15%।

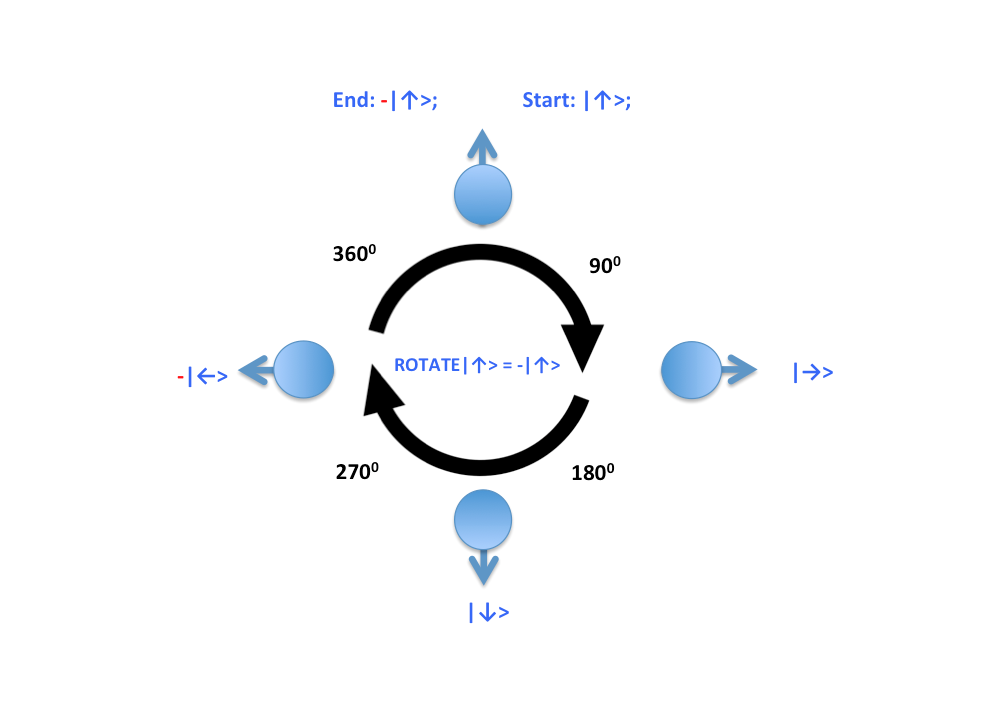
কণাদের স্পিন অনেকটা চুম্বকের মেরুর মতো। কম্পাসের কাঁটা যেমন চুম্বকের প্রভাবে নড়ে ওঠে, ঠিক একইভাব চুম্বক ব্যবহার করে কণাদের স্পিন পরিবর্তন করা সম্ভব। একটা 1/2-স্পিন কণা নেয়া যাক যার স্টেট ।↟>; এবার কণাটির স্পিন যদি ঘড়ির কাঁটার দিকে 90° ঘুরিয়ে দেয়া হয়, তবে আপডেট-রুল-১ অনুসারে কণাটির স্টেটে পরিবর্তন হবে এরকম:

।↟> —> s।↟> + s।↡> = ।↠>; অর্থাৎ, কণাটি নতুন স্পিন হবে ।↠>;

এই ।↠> স্টেটকে আবার ঘড়ির কাঁটার দিকে 90° ঘুরিয়ে দিলে স্পিনের নতুন স্টেট হবে: ।↡>;

এবার মজার ব্যাপার হলো, এই ।↡> স্টেটকে ঘড়ির কাঁটার দিকে আরো 90° ঘুরিয়ে দিলে স্পিনের নতুন স্টেট হবে:

।↡> —-> -s।↟> + s।↡> = -।↞>; কণাটি নতুন স্পিন হবে -।↞>;

লক্ষ্য করা দরকার যে, -।↞> এবং ।↠> দুটো সম্পূর্ণ ভিন্ন কোয়ান্টাম-স্টেট, তাই  -।↞> মানে ।↠> নয়। এবার একটি পূর্ণ 360° চক্কর সম্পন্ন করতে আমরা -।↞> স্টেটকে ঘড়ির কাঁটার দিকে শেষবার 90° ঘোরাবো, তাহলে নতুন স্টেট হবে -।↟>;

কণার শুরুর স্টেট ছিলো, ।↟>; কিন্তু, তার শেষে স্টেট হলো, -।↟>; অর্থাৎ, একটি 1/2-স্পিন কণাকে 360° ঘোরালে কণাটি তার শুরুর স্টেট হুবুহু ফেরৎ পায় না। আমরা বর্ন-রুলে দেখেছিলাম সম্ভাবনা নির্ণয়ে এম্প্লিটিউডের পরমমান নেয়া হয় ফলে স্টেটের এই (-) নেগেটিভ চিহ্ন সম্ভাবনা নির্ণয়ে কোনো প্রভাব ফেলে না। এমনকি, নেগেটিভ কিংবা পজিটিভ চিহ্ন স্টেটের কোনো ভৌত (Physical) পরিবর্তন সাধন করে না। অর্থাৎ, ।↟> এবং -।↟> দুটি একই স্টেট নির্দেশ করে। তাহলে, এই বাড়তি (-) চিহ্নের গুরুত্ব কোথায়?

বস্তুজগৎ (Macroscopic world) তুষারকণার-নীতি (Snowflake principle) অনুসরণ করে। ক্যালটেকের একদল গবেষক তুষারকণার ওপর ব্যাপক পরীক্ষণ চালিয়েছেন। তাদের সিদ্ধান্ত ছিলো প্রতিটি তুষারকণার ক্রিস্টাল কাঠামো ভিন্ন। ফলে, যেকোনো তুষারকণাকে আলাদাভাবে চিহ্নিত করা সম্ভব। একটা উদাহরণ দেয়া যাক, আপনার পকেটে যদি একই মানের দেখতে হুবুহু এক এমন দুটি মুদ্রা থাকে, তবে আপনি চাইলেই মাইক্রোস্কোপের মাধ্যমে মুদ্রার পৃষ্টের ঘষার দাগ বিশ্লেষণ করে মুদ্রা দুটির প্রত্যেককেই আলাদা আলাদাভাবে চিহ্নিত করতে পারবেন। ঘষার দাগ মুদ্রাদের জন্য একরকম সিরিয়াল নম্বর হিসেবে কাজ করে।

এবার, আপনাকে যদি দুটি ইলেক্ট্রন ধরিয়ে দেয়া হয়। তবে আপনার পক্ষে কোনো ইলেক্ট্রনকেই আলাদা আলাদাভাবে চিহ্নিত করা সম্ভব হবে না।  আপনি হয়তো সর্বোচ্চ বলতে পারবেন যে, কোন ইলেক্ট্রনের স্পিন কতো; কিন্তু, আমরা জানি স্পিন পরিবর্তন করা সম্ভব। তাই শুধুই স্পিন দিয়ে ইলেক্ট্রনদের আলাদা আলাদাভাবে চিহ্নিত করা সম্ভব নয়। এই ব্যাপারটি যেকোনো কণা এমনকি পরমাণু এবং অণুদের জন্যও প্রযোজ্য। অর্থাৎ, কণাদের এমন কোনো বৈশিষ্ট্যই নেই যেটা ব্যবহার করে প্রতিটি কণাকে আলাদা আলাদা পরিচয় দেয়া সম্ভব। কণাদের এই পরিচয় সঙ্কট সম্পর্কে সর্বপ্রথম ধারণা দেন মার্কিন পদার্থবিদ হোসায় উইলার্ড গিব্বস (Josiah Willard Gibbs)।

সমস্যাটি থার্মোডাইনামিক্সের। ধরুন, দুই প্রকোষ্ট বিশিষ্ট একটি সিলিন্ডার। প্রকোষ্ট দুটির মধ্যকার দেয়ালে একটি ভাল্ভ রয়েছে। এখন দুটি এক্সপেরিমেন্ট করা যাক। প্রথম এক্সপেরিমেন্টে আমরা একটি প্রকোষ্টে অক্সিজেন এবং অন্য প্রকোষ্টে নাইট্রোজেন গ্যাস দিয়ে পূর্ণ করবো। এবার যদি প্রকোষ্ট দুটির মধ্যকার ভাল্ভ খুলে দেয়া হয়, তবে পুরো সিলিন্ডার জুড়ে গ্যাসের মিশ্রণ ঘটবে। লক্ষ্য করার বিষয়টি হলো, সিলিন্ডারের ভাল্ভ খুলে দেবার আগে অবস্থা অর্থাৎ, গ্যাসদের পৃথক অবস্থা এবং ভাল্ভ খুলে দেবার পরে অবস্থা, অর্থাৎ, গ্যাসদের মিশ্রণ অবস্থা একেবারেই ভিন্ন। এই এক্সপেরিমেন্ট হলো অপরিবর্তনীয় বা ইররিভার্সিবল (Irreversible)। কারণ মিশ্রণ থেকে অক্সিজেন ও নাইট্রোজেনকে আলাদা করতে আমাদেরকে কাজ করতে হবে। এখন আমরা যদি অক্সিজেন বাদ দিয়ে প্রকোষ্ট দুটি শুধুই নাইট্রোজেন দিয়ে পূর্ণ করি এবং ভাল্ভটি খুলে দেই। তবে, ভাল্ভ খুলে দেবার আগে ও পরে সিলিন্ডারের অবস্থার কোনো পরিবর্তন আসবে না। আমরা যদি শত চেষ্টাও করি তবুও আমরা সিলিন্ডারের এই দুই অবস্থার মধ্যে কোনো পার্থক্য বের করতে পারবো না। তাই এই এক্সপেরিমেন্ট হলো পরিবর্তনীয় বা রিভার্সিবল (Reversible)। দ্বিতীয় এক্সপেরিমেন্টের এই রিভার্সিবিলিটি আমরা তখনই ব্যাখ্যা করতে পারি যখন আমরা ধরে নিই যে, নাইট্রোজেন অণুদের মধ্যে কোনো পার্থক্য নেই, তারা অভিন্ন (Indistinguishable)। সমজাতীয় গ্যাস অণুদের এই পরিচয় সঙ্কটকে বলে গিব্বস-প্যারাডক্স। এই গিব্বস-প্যারাডক্স সমাধান সম্ভব হয় কোয়ান্টাম-মেকানিক্সের অভিন্ন-কণা-তত্ত্বের (Theory of identical particle) মাধ্যমে।

গিব্বসে প্রথম থট-এক্সপেরিমেন্টটি কোয়ান্টাম-মেকানিক্সের মাধ্যমে করা যাক, ধরুন আমাদের কাছে দুটি কণা আছে, একটি প্রোটন এবং একটি ইলেক্ট্রন। এদের সম্মিলিত কোয়ান্টাম-স্টেট হবে: ।AB> এবং ।BA>; এখানে, ।AB> স্টেটে A হলো প্রোটন এবং B হলো ইলেক্ট্রন। এবং, ।BA> স্টেটে B হলো ইলেক্ট্রন এবং A হলো প্রোটন। যেহেতু, প্রোটন এবং ইলেক্ট্রনের ভর এবং চার্জ ভিন্ন তাই এরা সম্পূর্ণ আলাদা ধরণের কণা, তাই প্রোটনটিকে A এবং ইলেক্ট্রনটিকে B-এর মাধ্যমে চিহ্নিত করা সম্ভব। ফলে, ।AB> এবং ।BA> পুরোপুরি আলাদা দুটি কোয়ান্টাম-স্টেট। এবার, আমরা গিব্বসে দ্বিতীয় থট-এক্সপেরিমেন্টের মতোই দুটি অভিন্ন কণা, যেমন: দুটি ইলেক্ট্রন নিই তবে, ।AB> এবং ।BA> দুটোই একই কোয়ান্টাম-স্টেট হবে। কারণটা আগেই বলা হয়েছে যে, দুটো ইলেক্ট্রনকে কোনো ভাবেই আলাদা আলাদাভাবে চিহ্নিত করা যায় না। গাণিতিকভাবে SWAP-অপারেটর ব্যবহার করে আমরা এই অভিন্ন স্টেট দুটো প্রকাশ করতে পারি;

SWAP।AB> = ।BA>; কিংবা, SWAP।BA> = ।AB>;

SWAP-অপারেটরের কাজ হলো, কেটের (Ket) মধ্যে থাকা কণাজোড়াদের অবস্থান বিনিময় করা। এই SWAP-অপারেশনের ফলাফলের ওপর ভিত্তি করে আমাদের মহাবিশ্বের সমস্ত কণাদের দুইভাগে ভাগ করা যায়। প্রথম ফলাফল হলো,

SWAP।AB> = ।BA>;

অর্থাৎ, SWAP-অপারেশনের আগের এবং পরের স্টেট হুবুহু এক। এই দুটি কোয়ান্টাম-স্টেটকে আলাদা আলাদাভাবে প্রকাশ না করে একটি সুপারপজিশন-স্টেটের মাধ্যমে প্রকাশ করা যায়। এই সুপারপজিশন-স্টেটটি হলো, s।AB> + s।BA>; তাই এই কণাদের বলে প্রতিসম বা সিমেট্রিক কণা (Symmetric particles)। আমরা যদি, দুইবার SWAP-অপারেশন চালাই তবে;

SWAP^2।AB>

= SWAP(SWAP।AB>)

= SWAP।BA>

= ।AB>;

অর্থাৎ, দুটি SWAP-অপারেশন সিস্টেমকে হুবুহু আগের অবস্থায় নিয়ে যায়। এই ফলাফলকে বলে বোস-আইনস্টাইন-রুল (Bose Einstein rule) যে কণারা এই নিয়ম মেনে চলে তাদের আমরা বলি বোস-আইনস্টাইন কণা বা বোসন (Boson)। এই নিয়মের প্রস্তাব করেন ভারতীয়-বাঙালি সত্যেন্দ্রনাথ বসু এবং আইনস্টাইন।

অন্যদিকে, দ্বিতীয় ফলাফল হলো,

SWAP।AB> = -।BA>;

SWAP-অপারেশনে নতুন কোয়ান্টাম-স্টেটের এম্প্লিটিউড নেগেটিভ হয়। আমরা বর্ন-রুলে দেখেছি, নেগেটিভ-এম্প্লিটিউড সম্ভাবনা নির্ণয়ে কোনো প্রভাব বিস্তার করে না, কিংবা, ভিন্ন কোয়ান্টাম-স্টেটও নির্দেশ করা না। অর্থাৎ, ।AB> এবং -।BA> দুটোই একই কোয়ান্টাম-স্টেট নির্দেশ করে। তাই, এই দুটি কোয়ান্টাম-স্টেটকে আলাদা আলাদাভাবে প্রকাশ না করে মাত্র একটি সুপারপজিশন-স্টেটের মাধ্যমে প্রকাশ করা যায়। এই সুপারপজিশন-স্টেটটি হলো s।AB> – s।BA>; যদিও SWAP-অপারেশন এই কণাদের কোয়ান্টাম-স্টেটের পরিবর্তন ঘটায় না, তবুও ফলাফলে নেগেটিভ চিহ্নের কারণে এই কণাদের বলে অপ্রতিসম বা এন্টি-সিমেট্রিক কণা (Anti symmetric particles)। এবার যদি দুইবার SWAP-অপারেশন চালাই তবে;

SWAP^2।AB>

= SWAP(SWAP।AB>)

= SWAP(-।BA>) = -SWAP(।BA>)

= -(-AB>)

=।AB>;

অর্থাৎ, বোসনদের মতোই দুটি SWAP-অপারেশন সিস্টেমকে আগের অবস্থায় নিয়ে যায়। এই ফলাফলকে বলে ফার্মি-ডিরেক-রুল (Fermi Dirac rule)। যে কণার এই নিয়ম অনুসরণ করে তাদের আমরা বলি ফার্মি-ডিরেক কণা বা ফার্মিয়ন (Fermion)। এই নিয়মের প্রস্তাব করেন, ব্রিটিশ পদার্থবিদ পল-ডিরেক (Paul Dirac) এবং ইতালীর এনরিকো-ফার্মি (Enrico Fermi)।

দুটি SWAP-অপারেশন ফার্মিয়ানদের একটি অদ্ভুত বৈশিষ্ট্য প্রকাশ করে। সেটি হলো, দুটো অভিন্ন ফার্মিয়ন দিয়ে যদি একটি যৌগিক কণা তৈরি করা হয় তবে যৌগিক কণাটি হবে একটি বোসন। যেমন: হিলিয়াম পরমাণুতে রয়েছে দুটি প্রোটন, দুটি ইলেক্ট্রন, এবং দুটি নিউট্রন। বিশেষ অবস্থায় এই হিলিয়াম পরমাণু বোসনের মতো আচরণ করে। মূলত, ফার্মিয়ানদের এই বৈশিষ্ট্যের কারণে সুপারকন্ডাক্টর তৈরি করা সম্ভব হয়েছে। অন্যদিকে, বোসনদের কোনোভাবেই ফার্মিয়নে পরিণত করা যায় না।

তাহলে, বোসন এবং ফার্মিওনদের মধ্যে পার্থক্য কোথায়? শুধু একটি নেগেটিভ চিহ্নে। আমরা দেখবো এই নেগেটিভ চিহ্নের সাথে স্পিন স্টেটের নেগেটিভ চিহ্নের একটি রহস্যময় যোগাযোগ আছে।

ফোটনের অভিন্নতার ধারণাটি দেন সত্যেন্দ্রনাথ বসু ১৯২৪ সালে, প্রসঙ্গটা ছিলো ব্ল্যাকবডি রেডিয়েশন (Blackbody radiation)। যদিও ম্যাক্স প্লাঙ্ক এবং পরবর্তীতে আইনস্টাইন আলোর কোয়ান্টা সম্পর্কে ধারণা দেন, তবে সত্যেন্দ্রনাথ বসুই সর্বপ্রথম প্রস্তাব করেন যে আলোর এই কোয়ান্টাগুলো অভিন্ন। সত্যেন্দ্রনাথ বসু তার প্রস্তাবনা আইনস্টাইনের কাছে পাঠান এবং আইনস্টাইন বসুর এই ধারণাকে অন্যান্য কণা এমনকি অণু পর্যন্ত প্রসারিত করেন। সত্যেন্দ্রনাথ বসু এবং আইনস্টাইনের এই যৌথ ধারণাকে বলে বোস-আইনস্টাইন-রুল বা বোস-আইনস্টাইন-স্ট্যাটিস্টিক্স (Bose Einstein statistics)। সত্যেন্দ্রনাথ বসুর ধারণাটা ছিলো এরকম,

ধরুন, আমাদের কাছে আছে তিনটি বাক্স A, B, C এবং দুটি কণা। প্রথমে আমরা ধরে নেবো কণা দুটি ভিন্ন রকমের। আমরা যদি পরিমাপ করি তবে, বাক্স তিনটিতে কণাগুলো থাকার বেসিস-স্টেটগুলো হবে:

।AA>, ।BB>, ।CC>, ।AB>, ।BA>, ।AC>, ।CA>, ।BC>, এবং ।CB>; (মোট নয়টি)

এর মধ্যে প্রথম তিনটি স্টেট ।AA>, ।BB>, এবং ।CC> নির্দেশ করে যেকোনো একটি বাক্সে কণা দুটি থাকার এবং বাকি ছয়টি নির্দেশ করে ভিন্ন ভিন্ন বাক্সে কণা দুটি থাকার স্টেট। সুতরাং, কণারা ভিন্ন হবার কারণে একই বাক্সে কণা দুটি থাকার সম্ভাবনা হবে প্রায় (৩/৯ x ১০০)% = ৩৩%। এবার আমরা যদি দুটি অভিন্ন কণা নিই, তবে হিসাবটা হবে একটু ভিন্ন। আমরা জানি ।AB> এবং ।BA>; ।AC> এবং ।CA>; ।BC> এবং ।CB> স্টেটগুলো একই, তাই আলাদা আলাদাভাবে হিসেব না করে এদের সুপারপজিশন স্টেটগুলো হবে যথাক্রমে, s।AB> + s।BA>; s।AC> + s।CA>; এবং s।BC> + s।CB>; সুতরাং, অভিন্ন কণাদের ক্ষেত্রে সিস্টেমের বেসিস-স্টেটগুলো হবে:

।AA>, ।BB>, ।CC>, s।AB> + s।BA>, s।AC> + s।CA>, এবং s।BC> + s।CB>; (মোট ছয়টি)

প্রথম তিনটি আগের মতোই একই বাক্সে এবং শেষের তিনটি ভিন্ন বাক্সে কণা দুটি থাকার স্টেট নির্দেশ করে। তাই অভিন্ন কনার ক্ষেত্রে একই বাক্সে কণাদের পাওয়ার সম্ভাবনা (৩/৬ x ১০০)% = ৫০%। যেটা কিনা ভিন্ন ধরণের কণাদের চেয়ে বেশি। অর্থাৎ আমরা বলতে পারি, অভিন্ন বা প্রতিসমকণারা পরিসংখ্যানগতভাবে সামাজিক, এরা একসাথে থাকতে পছন্দ করে। ব্যাপারটা আরো পরিষ্কার হবে, যদি আমরা দুটির বদলে তিনটি কণা নিই। তিনটি ভিন্ন কণাদের ক্ষেত্রে, কণাদের মোট বেসিস-স্টেট ২৭টি, এরমধ্যে মাত্র তিনটি স্টেটে কণাদের একই বাক্সে পাওয়া যাবে। তাই, কণা তিনটিকে একসাথে পাওয়ার সম্ভাবনা (৩/২৭ x ১০০)% = ১১%। কিন্তু, কণার যদি প্রতিসম বা অভিন্ন হয় তবে, সিস্টেমের বেসিস-স্টেট হবে মোট ১০টি। এবং কণা তিনটিকে একসাথে পাওয়ার সম্ভাবনা হবে (৩/১০ x ১০০)% = ৩৩%। যেটা কিনা ভিন্ন কণাদের তিনগুণ।

বোস-আইনস্টাইন-রুল বা বোস-আইনস্টাইন-স্টাটিস্টিক্সের তিনটি উল্লেখযোগ্য ব্যবহার হলো, অনুপ্রাণিত-নিঃসরণ বা স্টিমুলেটেড-এমিশন (Stimulated emission), সুপারফ্লুইড (Superfluid), এবং সুপারকন্ডাক্টিভিটি (Superconductivity)।

ফোটনের নিঃসরণ তিন ধরণের হতে পারে। অবসর্পশন-এমিশন (Absorption emission): নিম্নশক্তিস্তর থেকে উচ্চশক্তিস্তরে যাবার সময় ইলেক্ট্রন ফোটন শোষণের মাধ্যমে অবসর্পশন-এমিশন ঘটায়। স্পন্টেনিয়াস-এমিশন (Spontaneous emission): উচ্চশক্তিস্তর থেকে নিম্নশক্তিস্তরে যাবার সময় ইলেক্ট্রন স্বতঃস্ফূর্ত ফোটন বিকিরণের মাধ্যমে স্পন্টেনিয়াস-এমিশন ঘটায়। তৃতীয়টি হলো, স্টিমুলেটেড-এমিশন: আইনস্টাইন ১৯২৭ সালে এ সম্পর্কে ধারণা দেন। উচ্চশক্তিস্তরে থাকা ইলেক্ট্রনদের ফোটন নিঃসরণে অনুপ্রাণিত করা যায়। স্টিমুলেটেড-এমিশন প্রক্রিয়ায়, উচ্চশক্তির ইলেক্ট্রন ফোটনের উপস্থিতিতে ঐ ফোটনের সমান শক্তির ফোটন নিঃসরণের মাধ্যমে নিম্নশক্তিস্তরে ফিরে যায়। ইলেক্ট্রনের স্টিমুলেটেড-এমিশন একটি কোয়ান্টাম ঘটনা যেটা বোস-আইনস্টাইন-স্টাটিস্টিক্সের মাধ্যমে ব্যাখ্যা করা যায়। আইনস্টাইনের এই স্টিমুলেটেড-এমিশন ধারণার ওপর ভিত্তি করে ১৯৬০ সালের দিকে লেসার (LASER = Light Amplification by Stimulated Emission of Radiation) তৈরি করা হয়।

বর্তমানে লেসার বিভিন্নভাবে তৈরি করা সম্ভব। এখানে স্টিমুলেটেড-এমিশন ব্যাখ্যার জন্য একটি প্রাথমিক পদ্ধতি দেখানো হলো। লেসার যন্ত্রে দুটি আয়না থাকে, এর মধ্যে একটি পূর্ণপ্রতিফলক এবং অন্যটি অর্ধপ্রতিফলক। এই দুই আয়নার মাঝে থাকে কিছু গ্যাস। এই গ্যাস অণুদের প্রথমে উদ্দীপ্ত করা হয়, একে বলে অপ্টিক্যাল-পাম্পিং (Optical pumping)। অপ্টিক্যাল-পাম্পিংয়ে  রাসায়নিক, বা ইলেক্ট্রিক-ডিসচার্জ, বা তীব্র আলোর মাধ্যমে গ্যাস অণুর ইলেক্ট্রনদের উচ্চশক্তিস্তরে নিয়ে যাওয়া হয়। যখন অধিকাংশ অণু উদ্দীপ্ত হয়ে পরে তখন এই অবস্থাকে বলে পপুলেশন-ইনভার্শন (Population inversion)। এই উদ্দীপ্ত অণুর ইলেক্ট্রনদের ফোটন নিঃসরণে অনুপ্রাণিত করার জন্য কিছু ফোটনকে আয়না দুটোর মাঝে ছেড়ে দেয়া হয় (ছবিতে স্পন্টেনিয়াস ফোটন হিসেবে দেখানো হয়েছে)। এই ফোটনগুলোর কিছু অর্ধপ্রতিফলক আয়না দিয়ে বেরিয়ে যায়। আর কিছু ফোটন দুই আয়নাতে ক্রমাগত প্রতিফলিত হতে থাকে। এই প্রতিফলিত ফোটনের কারণে অনুপ্রাণিত হয়ে উচ্চশক্তিস্তরে থাকা ইলেক্ট্রনগুলো এই প্রতিফলিত  ফোটনগুলোর সমান শক্তির ফোটন নিঃসরণ করতে থাকে। এই নিঃসরিত ফোটনগুলোর কোয়ান্টাম-স্টেট প্রতিফলিত ফোটনের সমান হয়। ফলে, নিঃসরিত ফোটনগুলো তীব্র একমুখী আলোকরশ্মি তৈরি করে, একে বলে কোহেরেন্ট-লাইট (Coherent light)।

আগেই বলা হয়েছিলো যে, হিলিয়াম বিশেষ অবস্থায় বোসনের মতো আচরণ করে। হিলিয়ামকে যদি ৪ ডিগ্রী কেলভিন তাপমাত্রায় রেখে দেয়া হয়, তবে হিলিয়াম তরলে পরিণত হবে, একে বলে হিলিয়াম-১ বা “He I” (এটা কিন্তু সমাণু বা আইসোটোপ না)। তাপমাত্রা আরো কমিয়ে যদি ২ ডিগ্রী কেলভিনে নিয়ে আসা হয়, তবে হিলিয়াম পরিণত হয় সুপারফ্লুইড হিলিয়ামে বা He II তে (এটাও কিন্তু সমাণু বা আইসোটোপ না)। সুপারফ্লুইডের অণু বোসনের মতো আচরণ করে তাই সুপারফ্লুইডের অণুগুলো বোসনদের মতোই সামাজিক এবং একই কোয়ান্টাম-স্টেটে থাকে। সাধারণ তরলের অণুদের মতো সুপারফ্লুইডের অণুগুলো ধাক্কাধাক্কি করে না, ফলে সুপারফ্লুইডের চলন ঘর্ষণহীন এবং এর তাপ-পরিবাহীতা (Thermal conductivity) অসীম।

কিছু কিছু বিদ্যুৎ পরিবাহীকে অতিনিম্ন তাপমাত্রায় নিয়ে আসা হলে, পরিবাহীর ইলেক্ট্রনগুলো জোড়ায় জোড়ায় মিলিত হয়ে একই কোয়ান্টাম-স্টেটে পৌঁছে। এই ইলেক্ট্রন জোড়াদের বলে কুপার-পেয়ার (Cupper pair)। এই কুপার-পেয়ারগুলো বোসন কণার মতো আচরণ করে। বোসনদের মতো ঘর্ষণহীন কুপার-পেয়ারগুলো পরিবাহীর মধ্যে দিয়ে চলার সময় একে অন্যকে ধাক্কা দেয়া না, তাই পরিবাহীতে কোনো রোধ বা রেসিস্টেন্স (Resistance) তৈরি করে না। এই রোধবিহীন পরিবাহিতাকে বলে সুপারকন্ডাক্টিভিটি। সুপারকন্ডাক্টিভিটি আবিষ্কৃত হয় ১৯১১ সালে, কিন্তু, এর ব্যাখ্যা দেয়া সম্ভব হয় ১৯৫০ সালের দিকে BCS-তত্ত্বের মাধ্যমে। সুপারকন্ডাক্টিভিটির এই BCS-তত্ত্বের প্রস্তাব করেন জন বার্ডেন (John Bardeen), লিওঁ কুপার (Leon Cupper), এবং জন স্ক্রিফার (John Schrieffer)।

সুপারফ্লুইডের অণুগুলো বা সুপারকন্ডাক্টরের কুপার-পেয়ারগুলো যে কোয়ান্টাম ঘটনা প্রকাশ করে তাকে বলে বোস-আইনস্টাইন-কনডেনসেট  বা BEC (Bose Einstein condensate)। বোস-আইনস্টাইন-কনডেনসেট সর্বপ্রথম স্বতন্ত্রভাবে প্রমাণিত হয় ১৯৯৫ সালে রুবিডিয়াম মৌলের মাধ্যমে। প্রথমে রুবিডিয়াম অণুদের পরীক্ষণ যন্ত্রে ভাসমান অবস্থায় রাখা হয়। এরপর লেসারের মাধ্যমে অণুদের তাপমাত্রা ১ডিগ্রী কেলভিনের দশ লক্ষভাগের একভাগে নামিয়ে আনা হয়। এই অতিনিম্ন তাপমাত্রায় কোটি কোটি রুবিডিয়াম অণুগুলো একই সামঞ্জস্যপূর্ণ (Coherent) কোয়ান্টাম-স্টেটে পৌঁছে। কোহেরেন্ট-স্টেটে থাকা রুবিডিয়াম অণুগুলো বোসনের মতো আচরণ করে।

আবার আসা যাক সেই, তিনটি বাক্স, A, B, C এবং দুটি কণার এক্সপেরিমেন্টে। তবে, এবার কণা দুটি অভিন্ন ফার্মিয়ন, যেমন: দুটো ইলেক্ট্রন। আমরা দেখেছিলাম, বোসনদের জন্য মোট ছয়টি বেসিস-স্টেট ছিলো, তার মধ্যে প্রথম তিনটি স্টেট ।AA>, ।BB>, এবং ।CC> ছিলো একই বাক্সে দুটো কণাকেই একসাথে থাকার স্টেট। কিন্তু, ফার্মিয়নদের ক্ষেত্রে এই তিনটি স্টেট বৈধ নয়। কারণ, ইলেক্ট্রনেরা অভিন্ন কণা তাই, SWAP-অপারেশন চালালে আমরা একই স্টেট ফেরৎ পাবো, যেমন:

SWAP।AA> = ।AA>; বা SWAP।BB> = ।BB>; কিংবা SWAP।CC> = ।CC>;

কিন্তু, ফার্মি-ডিরেক-রুল অনুসারে, ফার্মিয়নদের জন্য আমাদের পাওয়ার কথা অপ্রতিসম স্টেট যেমন:

SWAP।AA> = -।AA>; বা SWAP।BB> = -।BB>; কিংবা SWAP।CC> = -।CC>;।

তাই, ।AA>, ।BB>, এবং ।CC> স্টেট তিনটি ফার্মিয়নদের জন্য প্রযোজ্য নয়। এর মানেটা হলো, একই বাক্সে একসাথে দুটি ইলেক্ট্রন পাওয়া অসম্ভব। সুতরাং, আমাদের এক্সপেরিমেন্টে ইলেট্রন দুটোর বেসিস-স্টেট মাত্র তিনটি:

s।AB> – s।BA>; s।AC> – s।CA>; এবং s।BC> – s।CB>;

এই তিনটি স্টেট ভিন্ন ভিন্ন বাক্সে ইলেক্ট্রন দুটো থাকার স্টেট নির্দেশ করে। ঐতিহাসিকভাবে ফার্মি এবং ডিরেকের আগেই ১৯২৫ সালে অস্ট্রিয়ান পদার্থবিদ উল্ফগ্যাং-পাউলি (Wolfgang Pauli) পরমাণুর কাঠামো বিশ্লেষণে এই সিদ্ধান্তে পৌঁছেন যে, পরমাণুর কোনো শক্তিস্তরে থাকা একাধিক ইলেক্ট্রনের শ্রোডনিগার স্থির-তরঙ্গ এক হতে পারবে, কিন্তু, ইলেক্ট্রনগুলোর স্পিন এক হতে পারবে না। পাউলি এই সিদ্ধান্তকে বলা হয় পাউলির-বর্জননীতি (Pauli exclusion principle)। এই নীতি সব ফার্মিয়নদের জন্য প্রযোজ্য। এর পরপরই ফার্মি এবং ডিরেক গাণিতিকভাবে পাউলির-বর্জননীতির ব্যাখ্যা দেন, যাকে বলে ফার্মি-ডিরেক-রুল বা ফার্মি-ডিরেক-স্ট্যাটিস্টিক্স (Fermi Dirac statistics)। পাউলির-বর্জননীতি মতোই ফার্মি-ডিরেক-রুল সব ফার্মিয়নের ওপর প্রযোজ্য।

রুশ রসায়নবিদ দিমিত্রি মেন্ডেলিভ (Dmitri Mendeleev) সর্বপ্রথম বিভিন্ন মৌলের রাসায়নিক বৈশিষ্ট্য অনুসারে পর্যায়-সারণী তৈরি করেন। কিন্তু, এই পর্যায়-সারণীর ব্যাখ্যা সম্ভব হয় পাউলির বর্জননীতির মাধ্যমে। পরমাণুর শক্তিস্তরগুলো গুচ্ছকারে থাকে, এই গুচ্ছদের  বলে শেল (Shell)। এই শেলগুলোকে K, L, M, N, O, P, এবং Q দ্বারা চিহ্নিত করা হয়। সবনিম্ন শেলে রয়েছে মাত্র একটি শক্তিস্তর, পরের শেলে চারটি, ইত্যাদি। পরমাণুর রাসায়নিক বৈশিষ্ট্য নির্ভর করে সর্বশেষ শেলের ইলেক্ট্রনের সংখ্যার ওপর। আর ইলেক্ট্রন কিভাবে পরমাণুর বিভিন্ন শেলগুলোতে বিন্যস্ত হয় সেটা পাউলির বর্জননীতির মাধ্যমে ব্যাখ্যা করা সম্ভব। যেমন: হাইড্রোজেন, লিথিয়াম, সোডিয়াম এদের শেষ সেলে মাত্র একটি ইলেক্ট্রন, তাই এদের রাসায়নিক বৈশিষ্ট্য এক, এবং এরা পর্যায়-সারণীতে একই কলামে (প্রথম) অবস্থান করে। একইভাবে, হিলিয়াম এবং নিয়নের শেষ শেল একেবারে কানায় কানায় পরিপূর্ণ, তাই এরা রাসায়নিক বিক্রিয়ায় অংশগ্রহণ করে না, এদের বলে নিষ্ক্রিয় গ্যাস। নিষ্ক্রিয় মৌলগুলো পর্যায়-সারণীর শেষ কলামের অবস্থান করে।

পাউলির বর্জননীতি পরমাণুর নিউক্লিয়াসের ক্ষেত্রেও অত্যন্ত সফলভাবে প্রয়োগ করা হয়, একে বলে নিউক্লিয়ার-শেল-মডেল (Nuclear shell model)। পরমাণুর নিউক্লিয়াসে প্রোটন ও নিউট্রনের আলাদা আলাদা শেল থেকে। যেহেতু, প্রোটন ও নিউট্রন ভিন্ন ধরণের কণা তাই এদের শেলগুলোর শক্তিমাত্রাও ভিন্ন। পাউলির বর্জননীতি অনুসারে এই শেলগুলোর শক্তিস্তরে একই স্পিনযুক্ত প্রোটন কিংবা নিউট্রন থাকতে পারে না। যেহেতু, প্রোটন ও নিউট্রনের ওপর প্রবলশক্তি (Strong nuclear force) প্রযোজ্য তাই নিউক্লিয়ার-শেল-মডেলের হিসাব নিকাশ ইলেক্ট্রন-শেল-মডেলের থেকে ভিন্ন। নিউক্লিয়ার-শেল-মডেল অনুসারে হিলিয়াম-৪ সমাণুটি প্রকৃতির সবচেয়ে স্থিতিশীল নিউক্লিয়াসের অধিকারী। এর দুটি বিপরীত স্পিনযুক্ত প্রোটন এবং নিউট্রন থাকে।

পদার্থ জায়গা দখল করে, এর কারণও পাউলির-বর্জননীতি। একটি পরমাণুর প্রায় ০.১ থেকে ০.৫ ন্যানোমিটার জায়গা দখল করে, আর এই জায়গার প্রায় এক ট্রিলিয়নভাগের একভাগ জায়গা দখল করে নিউক্লিয়াস। বাকি জায়গা সম্পূর্ণ ফাঁকা, ইলেট্রনেরা এই ফাঁকা জায়গায় অবস্থান করে। আমরা চাইলেও এই ফাঁকা জায়গা সংকুচিত করতে পারিনা। গ্যাসের ক্ষেত্রে অণুদের মাঝে প্রচুর ফাঁকা জায়গা থাকে, চাপ প্রয়োগের মাধ্যমে এই ফাঁকা জায়গা সংকুচিত করা যায়। কিন্তু, তরল বা কঠিন পদার্থের ক্ষেত্রে এই ফাঁকা জায়গা থাকেনা বললেই চলে। যেমন: লোহার ঘনত্ব ৮গ্রাম/কিউবিক-সেন্টিমিটার। পৃথিবীর কেন্দ্রে লোহা প্রায় ৩ মিলিয়ন বায়ুমণ্ডলীয় চাপে থাকে। এই প্রচন্ড চাপে লোহার ঘনত্ব বৃদ্ধি পায় মাত্র ৬০% থেকে ৭০%। এই চাপ লোহার ঘনত্ব প্রায় ১৩গ্রাম/কিউবিক-সেন্টিমিটার। পদার্থের জন্য পাউলির-বর্জননীতি একটি অখণ্ডণীয় নীতি। প্রচন্ড চাপে পদার্থ প্রথমে তার শেলগুলোতে কোনো শূন্যস্থান থাকলে তাতে ইলেক্ট্রন পূরণ করতে থাকে। এর পরও যদি চাপ বাড়তে থেকে তবে পদার্থ পরিণত হয় ডিজেনারেটেড-ম্যাটারে (Degenerated matter)।

এখানে মনে রাখা দরকার, বোস-আইনস্টাইন-রুল বা ফার্মি-ডিরেক-রুল কোনো শক্তির প্রভাবে ঘটে না। অর্থাৎ, কোনো শক্তির উপস্থিতির বা অনুপস্থিতির সাথে এই দুই নিয়মের কোনো সম্পর্ক নেই। আমরা দেখেছি বোসন এবং ফার্মিয়ন কণাদের পার্থক্যের কারণ একটি (-) নেগেটিভ চিহ্ন। যেটা দুটি অভিন্ন ফার্মিয়ন কণার কোয়ান্টাম-স্টেট অদলবদলে পাওয়া যায়, কিন্তু দুটি অভিন্ন বোসনের ক্ষেত্রে পাওয়া যায় না। ফার্মিয়নদের এই (-) নেগেটিভ চিহ্নের কারণ কি? ১৯৪০ সালে উল্ফগ্যাং-পাউলি সর্বপ্রথম এই (-) নেগেটিভ চিহ্নের উৎপত্তি সম্পর্কে ধারণা দেন। পাউলি বলেন, ফার্মিয়নদের কোয়ান্টাম-স্টেট বিনিময়ে উদ্ভূত (-) নেগেটিভ চিহ্নের কারণ ফার্মিয়নদের স্পিন। তাই ধারণাটি স্পিন-স্ট্যাটিস্টিক্স-কানেকশন (Spin statistics connection) নামে পরিচিত।

আমরা আগেই দেখেছিলাম, 1/2-স্পিনযুক্ত কণার স্পিনকে যদি চুম্বকক্ষেত্রে প্রভাবে 360° ঘুরিয়ে দেয়া হয়, তবে কণার স্টেট ।↟> পরিবর্তিত হবে নতুন স্টেট -।↟> তে; একে ROTATE-অপারেটের মাধ্যমে দেখানো যায় এভাবে:

ROTATE।↟> = -।↟>;

ROTATE-অপারেটেরের কাজ হলো কণার স্পিনকে 360° ঘুরিয়ে দেয়া। বোসনদের স্পিন পূর্ণসংখ্যা যেমন: 0, 1, বা 2 ইত্যাদি। তাই, বোসনের ক্ষেত্রে ROTATE-অপারেটের স্পিন পরিবর্তন করে না। অর্থাৎ, বোসনের জন্য

ROTATE।স্টেট> = ।স্টেট>;

অন্যদিকে, ফার্মিয়নদের স্পিন সবসময়ই (পূর্ণসংখ্যা/2) যেমন: 1/2, 3/2 ইত্যাদি। ফার্মিয়নের ক্ষেত্রে ROTATE-অপারেশনে পাওয়া যায়,

ROTATE।স্টেট> = -।স্টেট>;

এই ব্যাপারটি মার্খ-জেন্ডার-ইন্টারফেরোমিটারের মাধ্যমে সহজেই প্রমাণ করা যায়। তবে এই এক্সপেরিমেন্টে আমরা ব্যবহার করবো নিউট্রন। তাই ইন্টারফেরোমিটারের ফোটন-ডিটেক্টরের পরিবর্তে আমাদেরকে ব্যবহার করতে হবে নিউট্রন-ডিটেক্টর। কোনো কিছু না করলে ফলাফল হবে ফোটনের মতোই। অর্থাৎ, সব নিউট্রন সবুজ-ডিটেক্টরে পাওয়া যাবে। নীল-ডিটেক্টরে কোনো নিউট্রন পৌঁছুবে না।

এবার আমরা ইন্টারফেরোমিটারের দ্বিতীয় বিম-স্প্লিটার এবং দ্বিতীয় আয়নার মাঝামাঝি একটি চুম্বক বসাবো যার কাজ নিউট্রনের স্পিন বিভিন্ন কোণে ঘুরিয়ে দেয়া। আমরা যদি চুম্বকের মাধ্যমে নিচের নিউট্রনের স্পিন 360° ঘুরিয়ে দেই, তবে নিউট্রন হবে ইনভার্টেড (ছবিতে (-) চিহ্নের মাধ্যমে দেখানো হয়েছে)। এই ইনভার্টেড নিউট্রনের কারণে দ্বিতীয় বিম-স্প্লিটারে নিউট্রনের ইন্টারফেরেন্স বিন্যাস পুরোপুরি পাল্টে যায়। ফলে, সব নিউট্রন নীল-ডিটেক্টরে পৌঁছুবে, সবুজ-ডিটেক্টরে কোনো নিউট্রন পাওয়া যাবে না। মজার ব্যাপার হলো, আমরা যদি নিউট্রনের স্পিন পুরো 720° বা দুইবার 360°-তে ঘুরিয়ে দেই, তবে নিউট্রন আবার পুরোনো ইন্টারফেরেন্স বিন্যাসে ফিরে যাবে, অর্থাৎ, নিউট্রন শুধু সবুজ-ডিটেক্টরে পাওয়া যাবে। স্পিন বিভিন্ন কোণে ঘোরানোতে সবুজ ডিটেক্টরে নিউট্রন পাওয়া সম্ভাবনা কতো সেটা নিচে টেবিলে দেখানো হলো। 180° এবং 540°-তে সবুজ এবং নীল ডিটেক্টর দুটোরই সম্ভাবনা ৫০%, অর্থাৎ, এই দুই কোণে নিউট্রনের ইন্টারফেরেন্স সম্পূর্ণ অনুপস্থিত। এর কারণটা হলো, এই দুই কোণের ক্ষেত্রে নিউট্রন ওপর না নিচের পথ ধরে এসেছে সেটা স্পিনের মাধ্যমে জানা যায়। অর্থাৎ, স্পিন নিউট্রনের যাত্রাপথের তথ্য বহন করে, বলা যায় স্পিন এক্সপেরিমেন্ট পরিমাপের কাজ করে। ফলে, সিস্টেমের পরিবর্তন হয় আপডেট-রুল-২ এর মাধ্যমে, তাই এক্সপেরিমেন্ট থেকে সুপারপজিশন এবং সেইসাথে ইন্টারফেরেন্স হারিয়ে যায়।

স্পিন-স্ট্যাটিস্টিক্স-কানেকশনে বলা হয় যে, দুটি ফার্মিয়ন তাদের কোয়ান্টাম -স্টেট বিনিময় করলে তাদের স্পিন 360° ঘুরে যায়। তাই SWAP-অপারেশনে (-) চিহ্নটি পাওয়া যায়। একইভাবে দুটি SWAP-অপারেশন চালালে তাদের স্পিন 720° ঘুরে যায় তাই তারা আগের স্টেটে ফিরে আসে। এই পর্যবেক্ষণের অর্থ কি দাঁড়ালো? আমরা বস্তুজগতে 360° ঘুরলে আবার আগের অবস্থানে ফিরে আসি। বোসনদেরও একই অবস্থা, কিন্তু, ফার্মিয়নদের জন্য দরকার 720°। এ থেকে আমরা এতটুকুই বলতে পারি যে, স্থানকাল সম্পর্কে বস্তুজগৎ এবং ফার্মিয়নের দৃষ্টিভঙ্গি অনেকখানি ভিন্ন।

আগের পর্ব: ডাবল-স্লিট এক্সপেরিমেন্ট: তরঙ্গ নাকি কণা?
পরের পর্ব: কোয়ান্টাম এনট্যাংলমেন্ট এবং EPR-পেপার

অবলম্বনে: “The Great Courses” থেকে প্রকাশিত “Quantum Mechanics: The Physics of the Microscopic World” by “Benjamin Schumacher”