ডাবল-স্লিট এক্সপেরিমেন্ট: তরঙ্গ নাকি কণা?

কণা এবং তরঙ্গ দুটি ভিন্ন জিনিস। কণার আছে, ভর (m) এবং বেগ (v)। এই দুটি বৈশিষ্ট্যের গুণফলকে বলে ভরবেগ বা মোমেন্টাম, p = mv। এই ভরবেগ হলো একটি বল বা ফোর্স (Force) যার দিক আছে, অর্থাৎ, ভরবেগ একটি ভেক্টর (Vector)। এই ভরবেগ যে শক্তির (E) সৃষ্টি করে সেটা হলো, E = 1/2mv^2 । অন্যদিকে, তরঙ্গের আছে তরঙ্গদৈর্ঘ্য (λ) এবং কম্পাঙ্ক (f), এই দুইয়ের গুণফলকে বলে তরঙ্গের গতি v = λf। প্রশ্ন হলো, আলো কি তরঙ্গ নাকি কণা?

থমাস ইয়াঙ (Thomas Young) ১৮০১ সালে তার বিখ্যাত ডাবল-স্লিট এক্সপেরিমেন্টের মাধ্যমে প্রমাণ করেন যে, আলো একটি তরঙ্গ। শুধু তাই নয়, ইয়াঙ আলোর তরঙ্গদৈর্ঘ্যও বের করার চেষ্টা করেন। তার হিসাব অনুসারে আলোর তরঙ্গদৈর্ঘ্য এক মাইক্রোনের চেয়েও ছোট। ডাবল-স্লিট এক্সপেরিমেন্টের মূল প্রতিপাদ্য ছিলো, আলো যখন পরীক্ষণ যন্ত্রের সূক্ষ্ম ফাঁক দুটির ওপর আপতিত হয়, তখন আলো দুটি আলাদা আলাদা তরঙ্গে বিভক্ত হয়ে যায়। এই দুটি তরঙ্গ যখন পর্যবেক্ষণ পর্দায় মিলিত হয় তখন পর্দায় উজ্জ্বল এবং অন্ধকারের ডোরাকাঁটা বিন্যাস দেখা যায়। পর্দার যে অংশে তরঙ্গ দুটির শিখর (Peak) মিলিত হয় সেখানে উজ্জ্বলতা দেখা যায়, একে বলে গঠনমূলক ব্যতিচার বা কন্সট্রাক্টিভ-ইন্টারফেরেন্স (Constructive interference)। এবং পর্দার যেখানে একটি তরঙ্গের শিখরের সাথে অন্য তরঙ্গের খাত (Trough) মিলিত হয় সেখানে দেখা যায় অন্ধকার, একে বলে ধ্বংসাত্মক ব্যতিচার বা ডেস্ট্রাক্টিভ-ইন্টারফেরেন্স (Destructive interference)। আপাত দৃষ্টিতে, আলোর এই ব্যতিচার বা ইন্টারফেরেন্স শুধুমাত্র তরঙ্গের মাধ্যমে ব্যাখ্যা করা সম্ভব।

অন্যদিকে, আইনস্টাইন ১৯০৫ সালে আলোক-বৈদ্যুতিক-প্রভাব বা ফটোইলেক্ট্রিক-ইফেক্ট (Photoelectric effect) ব্যাখ্যার মাধ্যমে আলোর কণা ধারণা প্রতিষ্ঠা করেন। ফটোইলেক্ট্রিক-ইফেক্টের মূল কথা ছিলো, কোনো নির্দিষ্ট কম্পাঙ্কের আলো যখন কোনো বিশেষ ধাতুর ওপর আপতিত হয় তখন ঐ ধাতু থেকে একটি নির্দিষ্ট শক্তির ইলেক্ট্রন বেরিয়ে যায়। আলোর তীব্রতা যদি বাড়িয়ে দেয়া হয় তবে বেরিয়ে যাওয়া ইলেট্রনের সংখ্যাও বৃদ্ধি পায়, কিন্তু ইলেক্ট্রনগুলোর শক্তি বাড়ে না। অন্যদিকে, যদি আলোর কম্পাঙ্ক বাড়িয়ে দেয়া হয় তবে, বেরিয়ে যাওয়া ইলেক্ট্রনগুলোর শক্তিও বেশি হয়। অর্থাৎ, আলোর প্রভাবে ধাতু থেকে নির্গত ইলেক্ট্রনের শক্তি নির্ভর করে আলোর কম্পাঙ্কের ওপর। আর, ইলেক্ট্রনের পরিমাণ নির্ভর করে আলোর তীব্রতার ওপর। আইনস্টাইনের ব্যাখ্যা ছিলো এরকম, একটি নির্দিষ্ট কম্পাঙ্কে আলোর একটি নির্দিষ্ট শক্তি থাকে। আলোর এই শক্তি বন্টিত হয় ছোট ছোট প্যাকেট বা কোয়ান্টা (Quanta) আকারে, যাদের বলা হয় ফোটন। ফোটন যখন ধাতুর পৃষ্টে আছড়ে পরে তখন একটি ফোটন শুধু একটি ইলেক্ট্রনকে আঘাত করে। উচ্চ কম্পাঙ্কের আলোর ফোটনগুলো উচ্চ শক্তিযুক্ত, ফলে এদের আঘাতে ইলেট্রনেরা উচ্চশক্তিতে বেরিয়ে যায়। অন্যদিকে, আলোর তীব্রতা বাড়ানোর সাথে সাথে ফোটনের সংখ্যা বৃদ্ধি পায়। আর, ফোটনের সংখ্যা বাড়ার সাথে সাথে বেরিয়ে যাওয়া ইলেক্ট্রনের সংখ্যাও বেড়ে যায়।

আইনস্টাইনের ফটোইলেক্ট্রিক-ইফেক্ট প্রমাণিত হবার সাথে সাথে জন্ম হয় আলোর তরঙ্গ-কণা-দ্বৈততা বা ওয়েভ-পার্টিকেল-ডুয়ালিটি (Wave particle duality)। অনেকেই এই পরস্পর বিপরীতমুখী দ্বৈততাকে ব্যাখ্যা করেন এভাবে, আলোর গতি হলো তরঙ্গের মতো, যেটা ডাবল-স্লিট এক্সপেরিমেন্টে দেখা যায়। কিন্তু, বস্তুর সাথে আলোর কার্যকলাপ (Interaction) হলো কণার মতো, যেটা ফটোইলেক্ট্রিক-ইফেক্টে দেখা যায়। ১৯২৪ সালে ফ্রেঞ্চম্যান লুই-ডি-ব্রোগ্লি (Louis de Broglie) এই ওয়েভ-পার্টিকেল-ডুয়ালিটিকে আলো থেকে পদার্থজগতেও টেনে আনেন। ব্রোগ্লি যেটা করেছিলেন সেটা হলো, কণার শক্তি এবং ভরবেগের সাথে তরঙ্গের কম্পাঙ্ক এবং তরঙ্গদৈর্ঘ্যের সম্পর্ক স্থাপন।

কণার শক্তি এবং তরঙ্গের কম্পাঙ্কের মধ্যে সম্পর্কটা পাওয়া যায় আইনস্টাইনের ফটোইলেক্ট্রিক-ইফেক্ট থেকে।

E = hf

আর, ব্রোগ্লির কণার ভরবেগ এবং তরঙ্গদৈর্ঘ্যের মধ্যে সম্পর্কটা এরকম,

p = h/λ

এখানে, E = শক্তি, h = প্লাঙ্ক ধ্রুবক, এবং f = আলোর কম্পাঙ্ক। h-এর মান 6.6x 10^(-34) জুল-সেকেন্ড।

ব্রোগ্লির এই ভরবেগ থেকে পদার্থের তরঙ্গদৈর্ঘ্য পাওয়ার উপযোগিতা কোথায়? ব্রোগ্লির সমীকরণ অনুসারে, পদার্থের তরঙ্গ হলো  স্থির-তরঙ্গ বা স্ট্যান্ডিং-ওয়েভ (Standing wave)। আর্নেস্ট রাদারফোর্ডের (Ernest rutherford) ১৯১১ সালে প্রস্তাবিত পরমাণুর সোলার-সিস্টেম মডেলের একটা বড় সমস্যা ছিলো। সমস্যাটা হলো, ইলেক্ট্রন হলো একটি চার্জযুক্ত কণা এবং বৃত্তাকার পথে আবর্তন হলো একধরণের ত্বরণ। ফলে, ইলেক্ট্রন যখন পরমাণুর নিউক্লিয়াসের চারিপাশে আবর্তিত হতে থাকে তখন ত্বরণ বজায় রাখার জন্য ইলেক্ট্রন শক্তি হারাতে থাকে। ইলেক্ট্রন থেকে এই শক্তি বেরিয়ে যায় বিদ্যুৎচুম্বকীয় তরঙ্গ আকারে। এক হিসাব অনুসারে, রাদারফোর্ড-মডেলে পরমাণুর ইলেক্ট্রনগুলো মাত্র কয়েক মাইক্রোসেকেন্ডের শক্তি হারিয়ে নিউক্লিয়াসে আছড়ে পরার কথা। পরমাণুর কাঠামোর এই অস্থিতিশীলতার সমস্যা সমাধানে নিলস বোর (Niels Bohr) ১৯১৩ সালে এগিয়ে আসেন ব্রোগ্লির তরঙ্গ সমীকরণ নিয়ে। পরমাণুর বোর-মডেল অনুসারে, নিউক্লিয়াসে চারিপাশের কক্ষপথগুলো আলাদা আলাদা শক্তিস্তর নির্দেশ করে। একেকটি শক্তিস্তরে হাতেগোনা কিছু স্থির-তরঙ্গ যুৎসই মতো ফিট (Fit) হতে বা মিলে যেতে পারে। এই স্থির-তরঙ্গগুলোর কিছু নির্দিষ্ট তরঙ্গদৈর্ঘ্য এবং কম্পাঙ্ক থাকতে পারে। যেই ইলেট্রনগুলোর শক্তি এবং ভরবেগ যথাক্রমে এই স্থির-তরঙ্গগুলোর কম্পাঙ্ক এবং তরঙ্গদৈর্ঘ্যের সাথে মিলে যায় শুধু সেই ইলেক্ট্রনগুলোই ঐ শক্তিস্তরে থাকতে পারবে। বিভিন্ন শক্তিস্তরের স্থির-তরঙ্গগুলোর কম্পাঙ্ক এবং তরঙ্গদৈর্ঘ্যগুলো ভিন্ন ভিন্ন হওয়ায় কারণে ইলেক্ট্রন যখন এক শক্তিস্তর থেকে অন্যশক্তি স্তরে যাওয়া আসা করে, ইলেক্ট্রনেরা তখন শক্তি শোষণ বা বর্জনের মাধ্যমে নিজেদের কম্পাঙ্ক গন্তব্য শক্তিস্তর অনুসারে খাপ খাইয়ে নেয়। নিউক্লিয়াসের কাছের কক্ষপথ নিম্নশক্তির এবং দূরবর্তী কক্ষপথগুলো উচ্চশক্তির। ফলে, ইলেক্ট্রন যখন উচ্চশক্তিস্তর থেকে নিম্নশক্তিস্তরে যায় তখন ইলেক্ট্রন শক্তি বের করে দেয় ফোটন নির্গমনের মাধ্যমে। আর, নিম্নশক্তিস্তর থেকে উচ্চশক্তিস্তরে যাবার সময় ইলেক্ট্রন শক্তি শোষণ করে ফোটন গিলে ফেলার মাধ্যমে। এই ফোটনগুলো শক্তি নির্ভর করে ইলেক্ট্রনগুলো বর্তমান এবং গন্তব্য শক্তিস্তর ওপর।

কোনো পরমাণুর ইলেক্ট্রনগুলোর বিভিন্ন শক্তিস্তরে লম্পঝম্পের ফলে নির্গত ফোটনগুলোর যে রঙিন বর্ণালী তৈরি করে তাকে বলে এমিশন-স্পেক্ট্রাম (Emission spectrum)। আর, ফোটন শোষণের ফলে যেই অন্ধকার ডোরাকাঁটা বিন্যাস দেখা যায় তাকে বলে অবসর্পশন-স্পেক্ট্রাম (Absorption spectrum)।

সমস্যা হলো, ব্রোগ্লির তরঙ্গ সমীকরণ ব্যবহার করে বোর শুধুমাত্রা হাইড্রোজেনের পারমাণবিক কাঠামো এবং এর স্প্রেক্ট্রাম সঠিকভাবে ব্যাখ্যা করতে পেরেছিলেন। কিন্তু, প্রবল চেষ্টার পরও বোর হাইড্রজেনের চেয়ে একটু জটিল পরমাণু হিলিয়ামের পারমাণবিক কাঠামো ঠিকমতো ব্যাখ্যা করতে পারেননি। শেষ পর্যন্ত এগিয়ে এলেন অস্ট্রিয়ান পদার্থবিদ এরউইন শ্রোডনিগার (Erwin Schrodinger) ১৯২৫ সালে তার বিখ্যাত তরঙ্গ-সমীকরণ নিয়ে। মজার ব্যাপার হলো, ব্রোগ্লির মতোই শ্রোডনিগারের সমীকরণ সমাধানে পাওয়া যায় স্থির-তরঙ্গ। এই শ্রোডনিগারের সমীকরণ ব্যবহার করে বোরের-মডেলের মাধ্যমে যেকোন পরমাণুর কাঠামো এবং স্প্রেক্ট্রাম ব্যাখ্যা করা সম্ভব হয়। শুধু সৌন্দর্য্যের কারণে শ্রোডনিগারের সমীকরণটি নিচে দেয়া হলো।

যা হোক, শ্রোডনিগারের সমীকরণের ব্যাপক সাফল্যের পর কোয়ান্টাম ফিজিক্সে তরঙ্গ-কণা-দ্বৈততা পাকাপোক্ত হলো। কিন্তু, সবচেয়ে বড় চমকটা নিয়ে এলেন ওয়ার্নার হেইজেনবার্গ (Warner Hesenburg) ১৯২৭ সালে।

তরঙ্গের একটা বৈশিষ্ট্য হলো, তরঙ্গ যখন প্রতিবন্ধক পদার্থের ফুঁটো কিংবা ফাঁক-ফোঁকরের মধ্যে দিয়ে চলার চেষ্টা করে তখন তরঙ্গের বিচ্ছুরণ ঘটে, এই বিচ্ছুরণকে বলে ডিফ্রাকশন (Diffraction) বা অপবর্তন। এই ডিফ্রাকশনের পরিমাণ নির্ভর করে প্রতিবন্ধক পদার্থের ফুঁটোর আকার এবং তরঙ্গদৈর্ঘ্যের ওপর। ফুঁটোটি যদি তরঙ্গদৈর্ঘ্যের চেয়ে ছোট হয় তবে ডিফ্রাকশনের পরিমাণ বেশি হবে। আর উল্টোটি হোলে ডিফ্রাকশনের পরিমাণ কম হবে। উদাহরণ হিসেবে একটা ইলেক্ট্রন ধরা যাক। ওপারের সিঙ্গেল-স্লিট এক্সপেরিমেন্টে দেয়ালটির গায়ে একটি ফুঁটো আছে। ধরা যাক, এই ফুঁটোর আকার ∆x  খুব ছোট (ওপরে বাঁয়ের ছবি)। যদি ইলেক্ট্রনটি এই ফুঁটো দিয়ে বেরিয়ে যায় তবে আমরা প্রায় নিশ্চিতভাবে বলতে পারবো ইলেক্ট্রনটির অবস্থান ছিলো ঐ ∆x-এ। এখন সমস্যা হলো, শ্রোডনিগারের সমীকরণ অনুসারে, ইলেক্ট্রন যখন তরঙ্গের মতো ফুঁটো দিয়ে বেরিয়ে যাবে তখন এই ইলেক্ট্রন-তরঙ্গের ডিফ্রাকশন ঘটবে। ফলে, ইলেক্ট্রন-তরঙ্গটি ফুঁটোর চারপাশ ছড়িয়ে এমনভাবে বিচ্ছুরিত হবে যে ইলেক্ট্রনের ভরবেগ কোন দিকে  সেটা নিশ্চিতভাবে বলা অসম্ভব। এবার, যদি  ফুঁটোর আকার বড় করা হয় (ওপরে ডানের ছবি), তবে ডিফ্রাকশন ঘটবে না এবং ইলেক্ট্রন-তরঙ্গটি সোজাসুজি ফুঁটো দিয়ে বেরিয়ে যাবে, ফলে আমরা নিশ্চিতভাবে ইলেক্ট্রনের ভরবেগ জানতে পারবো। কিন্তু, ফুঁটোর আকার বড় হওয়ায় ফুঁটোর কোন অংশ দিয়ে ইলেক্ট্রনটি বেরিয়ে গেছে সেটা আমরা বলতে পারবো না। অর্থাৎ, যখনই কণাকে আমরা তরঙ্গ হিসেবে গণ্য করি, ডিফ্রাকশনের কারণে কণা অবস্থান এবং ভরবেগ নির্ণয় এ দুটোর মধ্যে একপ্রকার আপোষ করতে হয়। অবস্থান নিশ্চিতভাবে নির্ণয় করা গেলে ভরবেগ নিশ্চিত হওয়া যায় না, এবং উল্টোটাও সত্যি। তরঙ্গ-কণা-দ্বৈততার কারণে তৈরি হওয়া এই অদ্ভুত অনিশ্চিয়তাকে হেইজেনবার্গ একটি সমীকরণে বন্দি করলেন, যাকে বলা হয়, হেইজেনবার্গের অনিশ্চিয়তার-নীতি।

∆x * ∆p ≥ ħ/2 

এখানে, ħ = h / 2π

কোয়ান্টাম ফিজিক্সের অদ্ভুত পর্যবেক্ষণগুলোর ব্যাখ্যায় বর্তমানে তিনটি মতবাদ প্রচলত আছে। নিলস বোরের কোপেনহেগেন-ইন্টারপ্রিটেশন, ডেভিড-বোহেমের (David Bohm) হিডেন-ভ্যারিয়াবল বা গোপন-চলরাশি তত্ত্ব (Hidden variable theory, ১৯৫২ সালে প্রকাশিত), এবং হিউ এভার্টের (Hugh Everett) বহুবিশ্ব তত্ত্ব ( Many world theory, প্রকাশিত ১৯৫৭ সালে)। হেইজেনবার্গের অনিশ্চিয়তার-নীতি আসলে কি বোঝায় সেই সম্পর্কে সবচেয়ে শক্তিশালী মতবাদটি হলো কোপেনহেগেন-ইন্টারপ্রিটেশন। বোরের মতে, কোয়ান্টাম-ফিজিক্সের এক্সপেরিমেন্টগুলোর পরিমাপ (Measurement) মোটেও পরোক্ষ কোনো প্রক্রিয়া নয়। পরিমাপ সরাসরি এক্সপেরিমেন্টের ফলাফলের ওপর প্রভাব বিস্তার করে। অর্থাৎ, এক্সপেরিমেন্টের ফলাফল নির্ভর করে পরিমাপের ওপর। আর মানব পরিসরে উপলব্ধির জন্য এই কোয়ান্টাম-এক্সপেরিমেন্টগুলোর ফলাফলকে বহুগুণে বিবর্ধিত করতে হয়। এসবের মানে হলো, প্রতিটি কোয়ান্টাম-এক্সপেরিমেন্ট অদ্বিতীয়। অর্থাৎ, আমরা যদি কণার অবস্থান নির্ণয়ে এক্সপেরিমেন্ট চালাই তবে অবস্হান নিশ্চিতভাবে জানতে পারবো। আর, যদি ভরবেগ নির্ণয়ের এক্সপেরিমেন্ট চালাই তবে আমরা নিশ্চিতভাবে কণার ভরবেগ জানতে পারবো। এক্সপেরিমেন্ট দুটি পুরোপুরি আলাদা এবং স্বতন্ত্র। এবং এক এক্সপেরিমেন্ট থেকে অন্য এক্সপেরিমেন্টের ফলাফল আশা করা যায় না। যতক্ষণ না আমরা যথাযত এক্সপেরিমেন্ট করছি ততক্ষণ কোয়ান্টাম জগতে কণাদের বিভিন্ন বৈশিষ্ট্যগুলোর মান অনির্ণেয় থেকে যায়। এই অনির্ণেয়তা প্রকৃতির ধর্ম, আমাদের অজ্ঞানতা নয়। পরিমাপের ওপর কোয়ান্টাম-এক্সপেরিমেন্টের ফলাফল নির্ধারণ হওয়ার ব্যাপারটিকে বলে কম্প্লিমেন্টারিটি-প্রিন্সিপল (Principle of complementarity) বা পরিপূরকতার-নীতি।

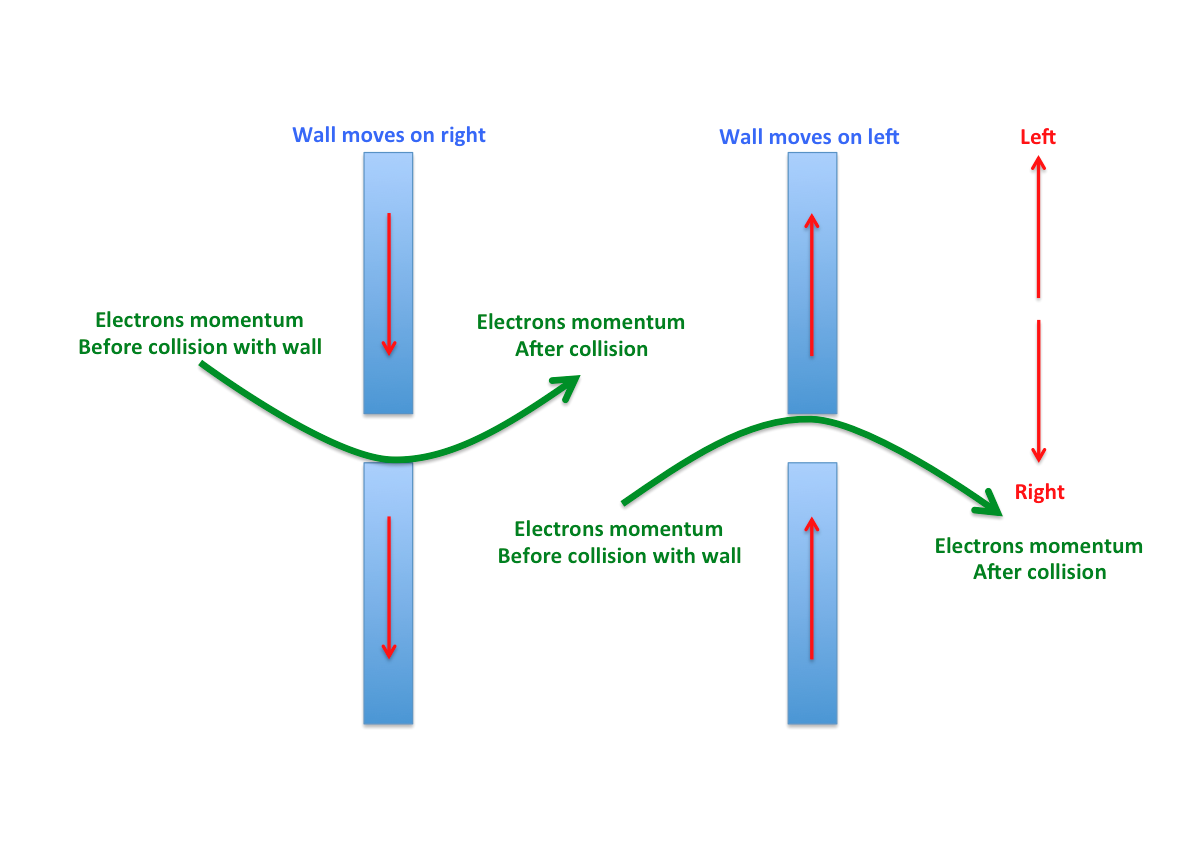
আইনস্টাইন কোয়ান্টাম জগতের এই অনির্ণেয়তাকে মেনে নিতে পারেননি। তার মতে, প্রকৃতিতে প্রতিটি কণার অবস্হান এবং ভরবেগ সুনির্দিষ্ট। আমাদের জ্ঞানের সীমাবদ্ধতার কারণে আমরা দুটোকে একসাথে নিখুঁতভাবে জানতে পারিনা। আইনস্টাইনের দৃঢ় বিশ্বাস জন্মে যে, কোয়ান্টাম-ফিজিক্স প্রকৃতিকে সঠিকভাবে ব্যাখ্যা করতে পারে না। এবং, তার এই বিশ্বাসের প্রতিফলন ঘটতে থাকে ১৯২৭ এবং ১৯৩০ সালের সলভেই-কনফারেন্সগুলোতে (Solvay conference)। এই দুই বছর কনফারেন্সের অবসর সময়ে আইনস্টাইন একের পর এক থট-এক্সপেরিমেন্টের মাধ্যমে কোয়ান্টাম-ফিজিক্সের অসংগতিগুলো তুলে ধরেছিলেন। আর নিলস বোর বহু চিন্তাভাবনা করে প্রতিটি থট-এক্সপেরিমেন্ট থেকে কোয়ান্টাম-ফিজিক্সকে রক্ষা করেছিলেন। হেইজেনবার্গের অনিশ্চিয়তার-নীতি নিয়ে আইনস্টাইনের একটা বিখ্যাত থট-এক্সপেরিমেন্ট ছিলো এরকম,

এক ফুঁটোর দেয়ালটিকে আমরা খুব হালকা বস্তু দিয়ে এমনভাবে তৈরি করবো যাতে দেয়ালটি পাশাপাশি (ডানে-বাঁয়ে) নড়াচড়া করতে পারে। ধরা যাক, দেয়ালের ফুঁটোটি খুব ছোট। এখন ইলেক্ট্রন যদি এই ফুঁটো ভেতর দিয়ে যাবার চেষ্টা করে, তবে কোনো কোনো সময় ইলেক্ট্রনটি ফুঁটোর কোণা বরাবর দেয়ালের সাথে ধাক্কা খাবে। ইলেক্ট্রন যদি ফুঁটোর বাঁয়ে ধাক্কা খায় তবে দেয়াল বাঁয়ে সরে আসবে এবং ইলেক্ট্রনের ভরবেগ ডানদিক বরাবর হবে। কিংবা, ইলেক্ট্রন যদি ফুঁটোর ডানে ধাক্কা খায়, তবে দেয়াল ডানে সরে আসবে এবং ইলেক্ট্রন ফুঁটোর বামদিক বরাবর বেরিয়ে যাবে। ফলে, ছোট ফুঁটোর কারণে আমরা ইলেক্ট্রনের প্রায় নিখুঁত অবস্থান জানতে পারবো এবং একইসাথে দেয়ালের নড়াচড়া থেকে ইলেক্ট্রনের ভরবেগও নিখুঁতভাবে জানতে পারবো। তাই, আইনস্টাইনের মতে হেইজেনবার্গের অনিশ্চিয়তার-নীতিতে আর কোনো অনিশ্চিয়তা রইলো না। বোর একটু সময় নিয়ে আইনস্টাইনের যুক্তির ফাঁক বের করেন। বোর বলেন, আইনস্টাইন দেয়ালের অনিশ্চিয়তার-নীতি হিসেবে আনতে ভুলে গেছেন। দেয়ালে ফুঁটোর অবস্থান যদি ∆X এবং দেয়ালের নড়াচড়া বা ভরবেগ যদি ∆Y ধরা হয়, তবে দেয়াল নিজেও অনিশ্চিয়তার-নীতি অনুসরণ করে। অর্থাৎ,  ∆X * ∆Y ≥ ħ/2। তাই, ইলেক্ট্রনের সাথে সাথে দেয়ালেরও অনিশ্চিয়তার-নীতি হিসেবে আনতে হবে। আইনস্টাইন বোরের যুক্তিটি মেনে নেন এবং অনিশ্চিয়তার-নীতির যথার্থতা স্বীকার করেন।

এই থট-এক্সপেরিমেন্টের মূল কথা হলো, হেইজেনবার্গের অনিশ্চিয়তার-নীতি প্রকৃতিতে সবার ওপরেই প্রযোজ্য। যদি কোনো কণা বা বস্তুর ক্ষেত্রে এর ব্যাতিক্রম ঘটতো তবে ঐ বস্তু ব্যবহার করে আমরা বাকি যেকোনো কণাকে অনিশ্চিয়তার-নীতি থেকে বের করে করে আনতে পারতাম।

হেইজেনবার্গের অনিশ্চিয়তার-নীতির আরেকটি রূপ আছে যার গুরুত্ব মহাজাগতিক পর্যায়ে।

∆t * ∆E ≥ ħ/2

এই অসমতাটি বলে, কোনো সুনির্দিষ্ট সময়ে কোনো কণার শক্তি সুনিশ্চিতভাবে নির্ণয় করা যায় না। একইভাবে, কোনো কণার শক্তি নিখুঁতভাবে নির্ণয় করা হলে কণাটি কতক্ষণ ঐ শক্তির অধিকারী ছিলো সেটা নিশ্চিতভাবে বলা যায় না। সময় এবং শক্তির এই অনিশ্চিয়তাই কোয়ান্টাম-ফ্লাকচুয়েশন (Quantum fluctuations) এবং শূন্যস্থানের-শক্তির (Vacuum energy) জন্য দায়ী।

এখন কণাদের তরঙ্গ বলতে কি বোঝায়? একটু বিস্তারিত বলা যাক, বাতাসের চাপের তারতম্যতাকে আমরা বলি শব্দ। একইভাবে, বিদ্যুৎচুম্বকীয়-ক্ষেত্র বা ইলেক্টোম্যাগ্নেটিক-ফিল্ডের পরিবর্তনশীল শক্তির ঢেউকে আমরা বলি আলো। কিন্তু, ইলেক্ট্রন-তরঙ্গ আবার কি জিনিস? জার্মান পদার্থবিদ ম্যাক্স বর্ন (Max Born) ১৯২৮ সালে প্রস্তাব করেন যে, শ্রোডনিগারের সমীকরণের ψ চিহ্নটি আসলে কণার তরঙ্গের বদলে কণাকে খুঁজে পাওয়ার সম্ভাবনা নির্দেশ করে। শ্রোডনিগারের সমীকরণের ψ চিহ্নটিকে বলা হতো ওয়েভ-ফ্যাংশন (Wave function), কিন্তু, বর্ন বলেন এই  ψ হলো প্রোবাবিলিটি-ফ্যাংশন (Probability function)। বর্নের মতে, ।ψ।^2 যেটা কিনা কোনো বিন্দুতে তরঙ্গের তীব্রতা নির্দেশ করে, এই ।ψ।^2 ই আসলে ঐ বিন্দুতে কণা খুঁজে পাবার সম্ভাবনা নির্দেশ করে। একে বলা হয় বর্নের-নিয়ম বা বর্ন-রুল (Born rule)।

আমরা আগে বলেছিলাম, ইয়াঙের ডাবল-স্লিট এক্সপেরিমেন্ট আলোর তরঙ্গ রূপ নিশ্চিতভাবে প্রমাণ করে। এবার দেখা যাক, বর্ন-রুল ব্যবহার করে তরঙ্গ-তত্ত্ব ছাড়াই কিভাবে আলোর ডাবল-স্লিট এক্সপেরিমেন্টটি ব্যাখ্যা করা যায়। রিচার্ড ফাইনম্যান বলেন, “আপনি যদি ডাবল-স্লিট এক্সপেরিমেন্টটি বুঝতে পারেন তবে আপনার কোয়ান্টাম-মেকানিক্স বোঝা শেষ।” কিন্তু, তিনি এটাও বলেছেন, “আমি নিশ্চিতভাবে বলতে পারি যে কেউই কোয়ান্টাম-মেকানিক্স বোঝেনা।” ফাইনম্যানের এই দুটি উদ্ধৃতি মেলালে সহজেই বোঝা যায় ডাবল-স্লিট এক্সপেরিমেন্টটি কতোটা দুর্বোধ্য। সৌভাগ্যক্রমে, ইয়াঙের ডাবল-স্লিট এক্সপেরিমেন্টের অতিসরল একটি সংষ্করণ আছে যেটা মার্খ-জেন্ডার ইন্টারফেরোমিটার (Mach–Zehnder interferometer) এক্সপেরিমেন্ট নামে পরিচিত।

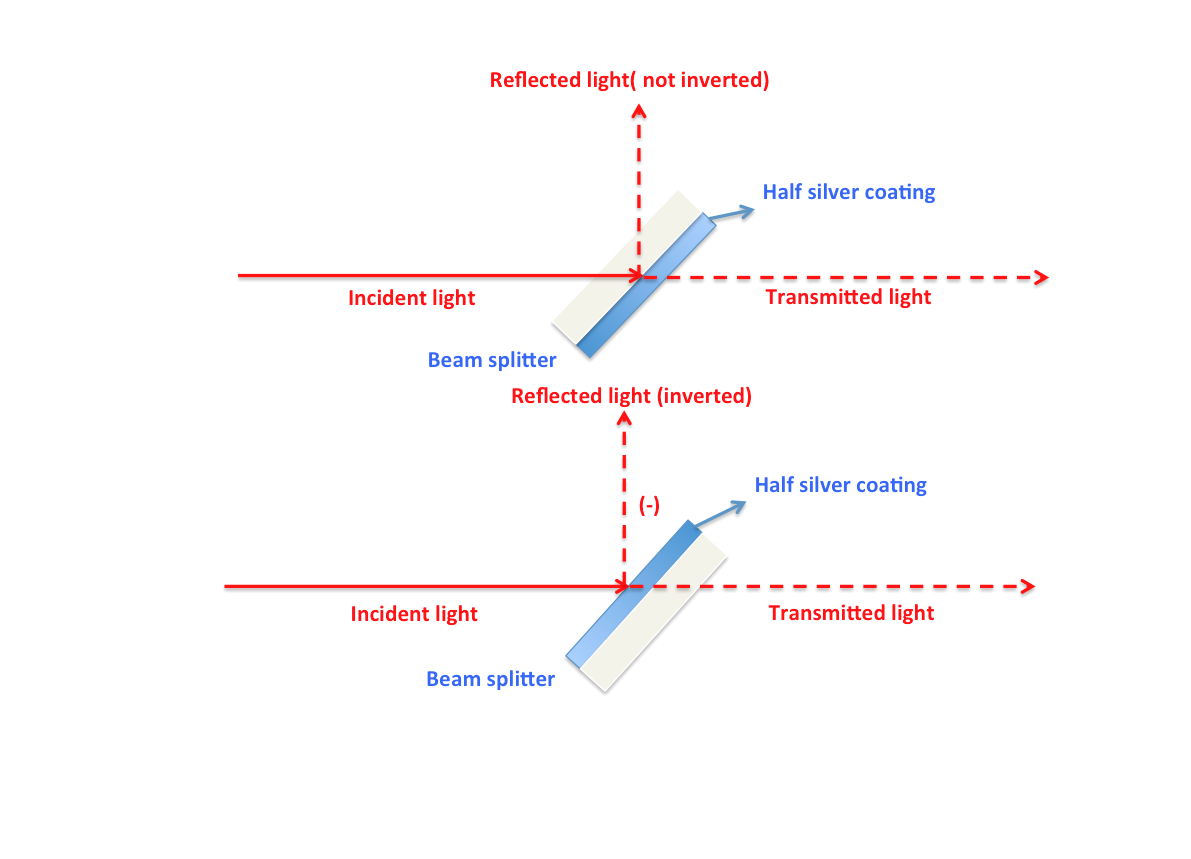
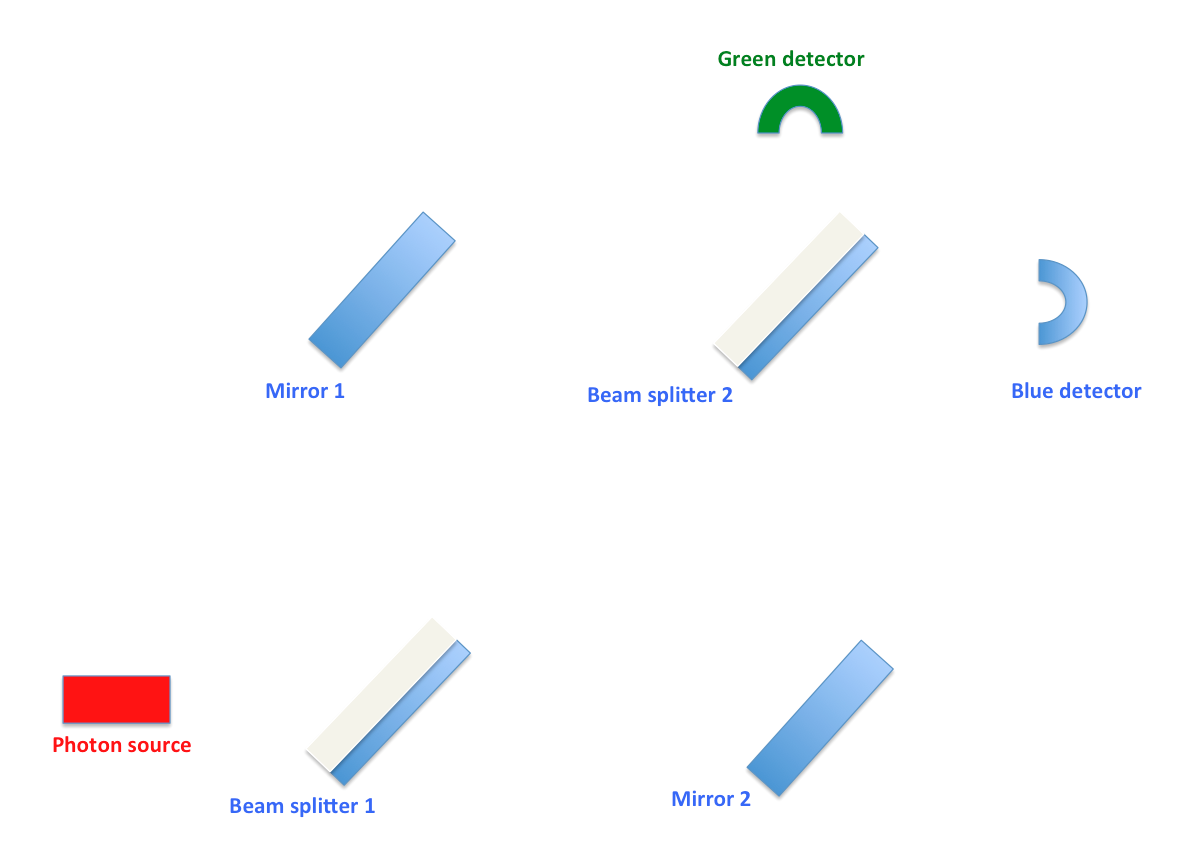
মার্খ-জেন্ডার ইন্টারফেরোমিটারে মাত্র তিনটি উপাদান আছে। দুটি আয়না, দুটি অতি সংবেদনশীল ফোটন-ডিটেক্টর, এবং দুটি বিম-স্প্লিটার (Beam splitter)। এই বিম-স্প্লিটারগুলো হলো স্বচ্ছ কাঁচ যাদের একপাশে রুপার অর্ধস্বচ্ছ প্রলেপ দেয়া থাকে। ফলে, আলোকরশ্মি যখন এই বিম-স্প্লিটারে আপতিত হয় তখন, আলোকরশ্মি বিভক্ত হয়ে অর্ধেক প্ৰতিফলিত হয়, বাকি অর্ধেক সরাসরি বিম-স্প্লিটার ভেদ করে চলে যায় (Transmitted beam)। এই বিম-স্প্লিটারের একটি অদ্ভুত বৈশিষ্ট্য হলো, আলোকরশ্মি যদি সরাসরি রুপার প্রলেপের ওপর আপতিত হয়, তবে প্রতিফলিত আলোকরশ্মির দশা বা ফেজ হয় ভেদকৃত আলোকরশ্মির ঠিক উল্টো বা ইনভার্টেড (Inverted), একে নেগেটিভ চিহ্ন (-) দিয়ে সূচিত করা হয়। এবার, যদি আলোকরশ্মির বদলে একটি ফোটন এই বিম-স্প্লিটারের মুখোমুখি হয় তবে ফোটনের দুটি উপায় আছে, হয় ফোটনটি প্রতিফলিত হবে, নয়তো ফোটনটি বিম-স্প্লিটার ভেদ করে বেরিয়ে যাবে। এই দুই উপায়ের প্রতিটির সম্ভাবনা ৫০%।

মার্খ-জেন্ডার এক্সপেরিমেন্টে আসার আগে কিছু কোয়ান্টাম-মেকানিক্সের শব্দ এবং ব্যাকরণ শেখা যাক। কোয়ান্টাম-মেকানিক্সে যেকোনো এক্সপেরিমেন্ট চালানো হয় একটি সিস্টেমের ওপর। আমাদের ক্ষেত্রে মার্খ-জেন্ডার ইন্টারফেরোমিটার এবং এর ভেতরের ফোটন হলো আমাদের কোয়ান্টাম-সিস্টেম, সংক্ষেপে সিস্টেম (System) । সিস্টেমে কণাদের অবস্থাকে বলে কোয়ান্টাম-স্টেট, সংক্ষেপে স্টেট (State)। স্টেট নির্দেশ করা হয় কেট (Ket) প্রতীক দিয়ে। কেট প্রতীকে যেকোনো কোয়ান্টাম-স্টেটকে একটি “।” এবং “>” চিহ্নের ভেতরে প্রকাশ করা হয়। যেমন: ।লেবেল>; একটি কোয়ান্টাম-স্টেট নির্দেশ করে, এখানে লেবেল হলো যেকোন অর্থবোধক শব্দ বা সংখ্যা।

একটি কোয়ান্টাম-সিস্টেমে একটি নির্দিষ্ট পরিমাপের (Measurement) জন্য দরকারি প্রতিটি আলাদা আলাদা সম্ভব্য কোয়ান্টাম-স্টেটদের সেটকে (Set)  বলে বেসিস-স্টেট (Basis state)। যেমন: ।লেবেল১> এবং ।লেবেল২>; এই সেটটি বেসিস-স্টেট নির্দেশ করে।

একটি কোয়ান্টাম-সিস্টেমে কণাদের একাধিক বেসিস-স্টেট থাকতে পারে। এই বেসিস-স্টেটগুলোর সমষ্টিকে বলে সুপারপজিশন-স্টেট (Superposition state)।  সুপারপজিশন-স্টেটে প্রতিটি বেসিস-স্টেটগুলোর আলাদা আলাদা সম্ভাবনা থাকে। এই সম্ভাবনা পাওয়া যায় একটি প্যারামিটার থেকে যার নাম বিস্তৃতি বা এম্প্লিটিউড (Amplitude)। একটি সুপারপজিশন-স্টেটের সমীকরণে কোনো স্টেটের এম্প্লিটিউডকে বর্গ করলে ঐ স্টেটের সম্ভাবনা পাওয়া যায়। যেকোনো সম্ভাবনার সর্বনিম্ন মান “শূন্য” এবং সর্বোচ্চ মান “এক”। কোনো স্টেটের সম্ভাবনা “শূন্য” মানে সিস্টেমকে নিশ্চিতভাবে ঐ স্টেটে পাওয়া যাবে না। আর, কোনো স্টেটের সম্ভাবনা “এক” মানে সিস্টেমকে অবশ্যই ঐ স্টেটে পাওয়া যাবে। এক্সপেরিমেন্ট চলার সময় ফোটনটি ইন্টারফেরোমিটারের কোথাও না কোথাও অবস্থান করে। তাই, একটি সিস্টেমের সব সম্ভাব্য স্টেটের সম্ভাবনাগুলোর সমষ্টি হবে “এক”। উদাহরণ:

a।লেবেল১> + b।লেবেল২>

ওপরের যোগফলটি একটি সুপারপজিশন-স্টেট নির্দেশ করে। এখানে, a হলো কোয়ান্টাম-স্টেট ।লেবেল১> এর এম্প্লিটিউড এবং ।a।^2 হলো সম্ভাব্যতা। একইভাবে b হলো কোয়ান্টাম-স্টেট ।লেবেল২> এর এম্প্লিটিউড এবং ।b।^2 হলো সম্ভাব্যতা। ।a।^2 + ।b।^2 = 1 হতে হবে।

মার্খ-জেন্ডার এক্সপেরিমেন্টে যেহেতু মাত্র দুটি সমান সম্ভাবনার পথ আছে, তাই সুবিধার জন্য আমরা এই পথ দুটিতে ফোটনের কোয়ান্টাম-স্টেটের এম্প্লিটিউডকে আমরা s = 1/√2 হিসেবে লিখতে পারি। হিসেব অনুসারে, ।s।^2 + ।s।^2 = ।1/√2।^2 + ।1/√2।^2 = 1/2 + 1/2 = 1, যেটা সুপারপজিশনের শর্ত পূরণ করে।

মজার ব্যাপার হলো, কোয়ান্টাম-মেকানিক্সে মাত্র ৫টি সাধারণ নিয়ম আছে। নিয়মগুলো এরকম,

(১) সুপারপজিশন নিয়ম (Rule of Superposition): এটি এসেছে কম্প্লিমেন্টারিটি-প্রিন্সিপল থেকে। এই নিয়ম অনুসারে, এক বা একাধিক বেসিস-স্টেট দিয়ে তৈরি সুপারপজিশন-স্টেটও একটি কোয়ান্টাম-স্টেট।

(২) সম্ভাবনার নিয়ম (Rule of Probability) বা বর্ন-রুল: এই নিয়মটি আমরা আগেই দেখেছিলাম। শ্রোডনিগারের সমীকরণের তরঙ্গ-তীব্রতা ψ কণার অবস্থানের সম্ভাব্যতা ।ψ।^2 নির্দেশ করে। গাণিতিকভাবে, সুপারপজিশন-স্টেটে কোনো নির্দিষ্ট স্টেটের এম্প্লিটিউডের পরমমানের বর্গ ঐ স্টেটের সম্ভাবনা নির্দেশ করে। পরমমান নির্দেশের জন্য আমরা দুটি “।” চিহ্নের মাঝে এম্প্লিটিউড প্রকাশ করা হয়। এই “।” চিহ্নের কারণে যেকোনো নেগেটিভ (-) চিহ্নকে উপেক্ষা করা হয়। যেমন:  “-0.2” যদি এম্প্লিটিউড নির্দেশ করে, তবে এ থেকে প্রাপ্ত সম্ভাবনা হবে, ।-0.2।^2 = 0.2^2 = 0.04।

(৩) হালনাগাদকরণ নিয়ম ১ বা আপডেট-রুল ১ (Update rule 1): দুটি আপডেট-রুল রয়েছে। কোনো ঘটনার সাথে সাথে কোয়ান্টাম-সিস্টেম কিভাবে পরিবর্তিত হয় সেগুলো আপডেট-রুল ব্যাখ্যা করে। আপডেট-রুল-১ অনুসারে, কোয়ান্টাম-সিস্টেমকে পরিমাপ করা না হলে, পরিবর্তনগুলো এমন সুনির্দিষ্টভাবে ঘটে যে পরিবর্তিত সিস্টেমের সুপারপজিশন-স্টেট বজায় থাকে।

(৪) হালনাগাদকরণ নিয়ম ২ বা আপডেট-রুল ২ (Update rule 2): কোয়ান্টাম-সিস্টেমকে পরিমাপ করা হলে, পরিবর্তিত সিস্টেমের নতুন কোয়ান্টাম-স্টেট নির্ভর করে পরিমাপের ওপর। পরিমাপের ফলে কোয়ান্টাম-স্টেটের পরিবর্তন ঘটে এলোমেলোভাবে (Randomly) যার ফলাফল নির্ভর করে ঘটনার সম্ভাব্যতার ওপর।

(৫) সংযুক্তির নিয়ম বা কম্পোসিশন রুল (Rule of composition): এই নিয়ম অনুসারে, দুই বা ততোধিক কণাদের সম্মিলিত কোয়ান্টাম-স্টেট কণাগুলোর কোয়ান্টাম-স্টেটগুলোর সরল গুণফল অথবা গুণফলের সুপারপজিশন-স্টেট। একই সিস্টেমের অন্তর্ভুক্ত কণার যদি এই কম্পোসিশন-রুল মেনে না চলে, তবে আমরা ঐ কণাদের স্টেটকে বলি এনট্যাংগেল্ড-স্টেট (Entangled state)। ধরা যাক, প্রথম কণার কোয়ান্টাম-স্টেট ।U> এবং দ্বিতীয় কণার a।V> + b।W>; কম্পোসিশন-রুল অনুসারে কণা দুটির সম্মিলিত কোয়ান্টাম-স্টেট হবে স্টেট দুটির সরল গুণফলের সমান বা গুণফলের সুপারপজিশনের-স্টেট, অর্থাৎ,  a।UV> + b।UW>;

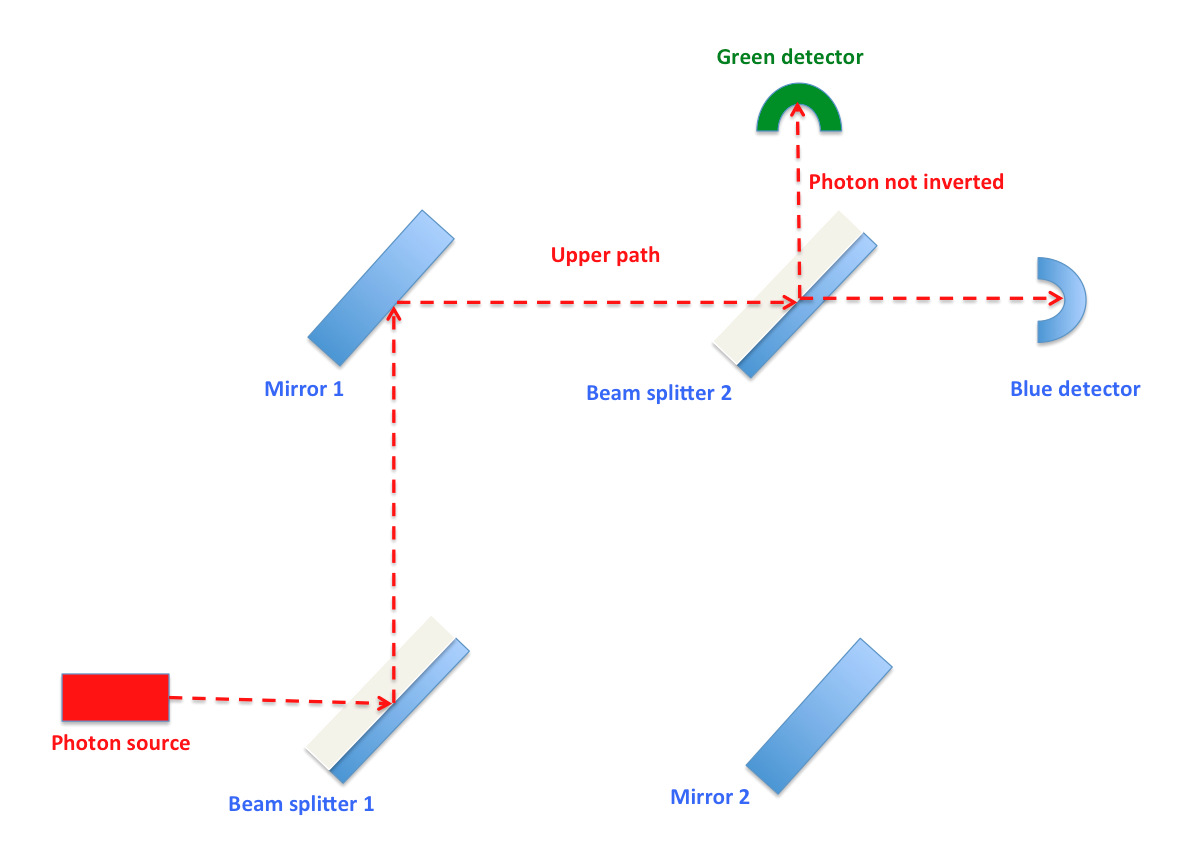
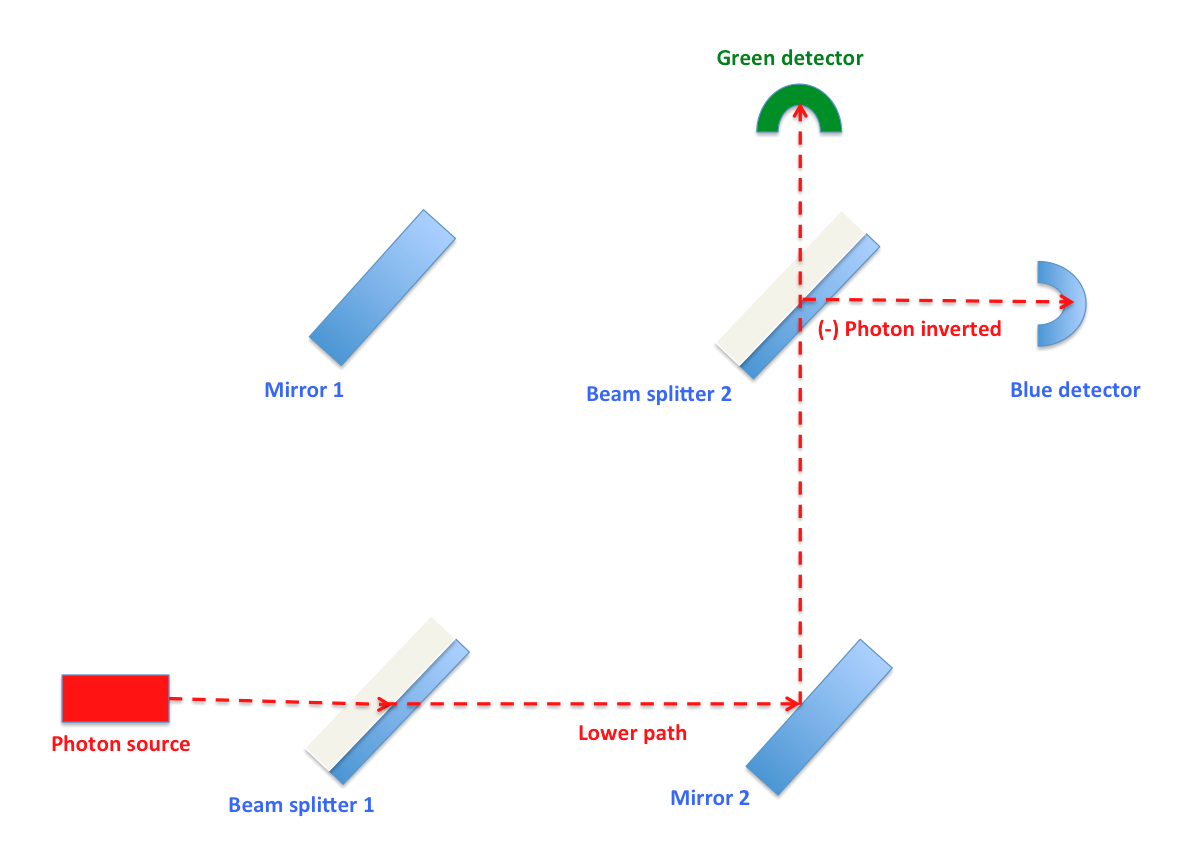
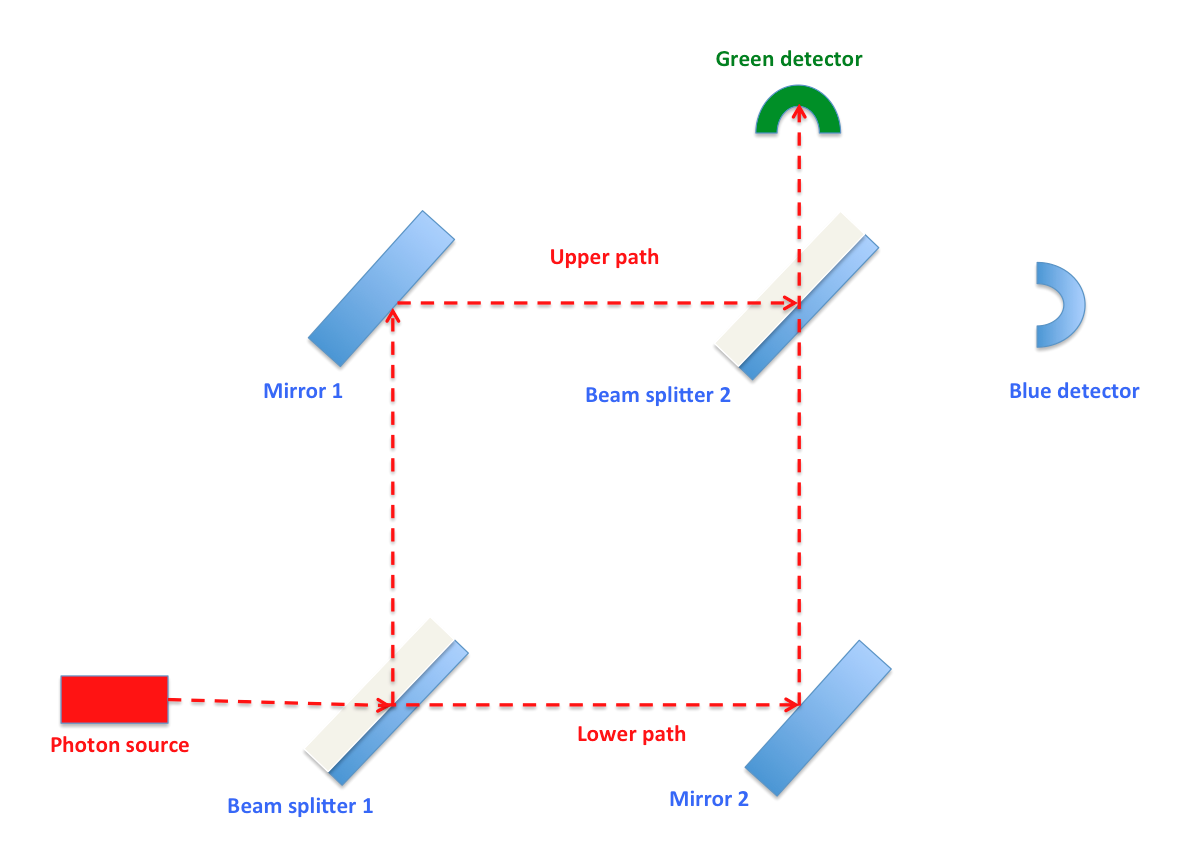
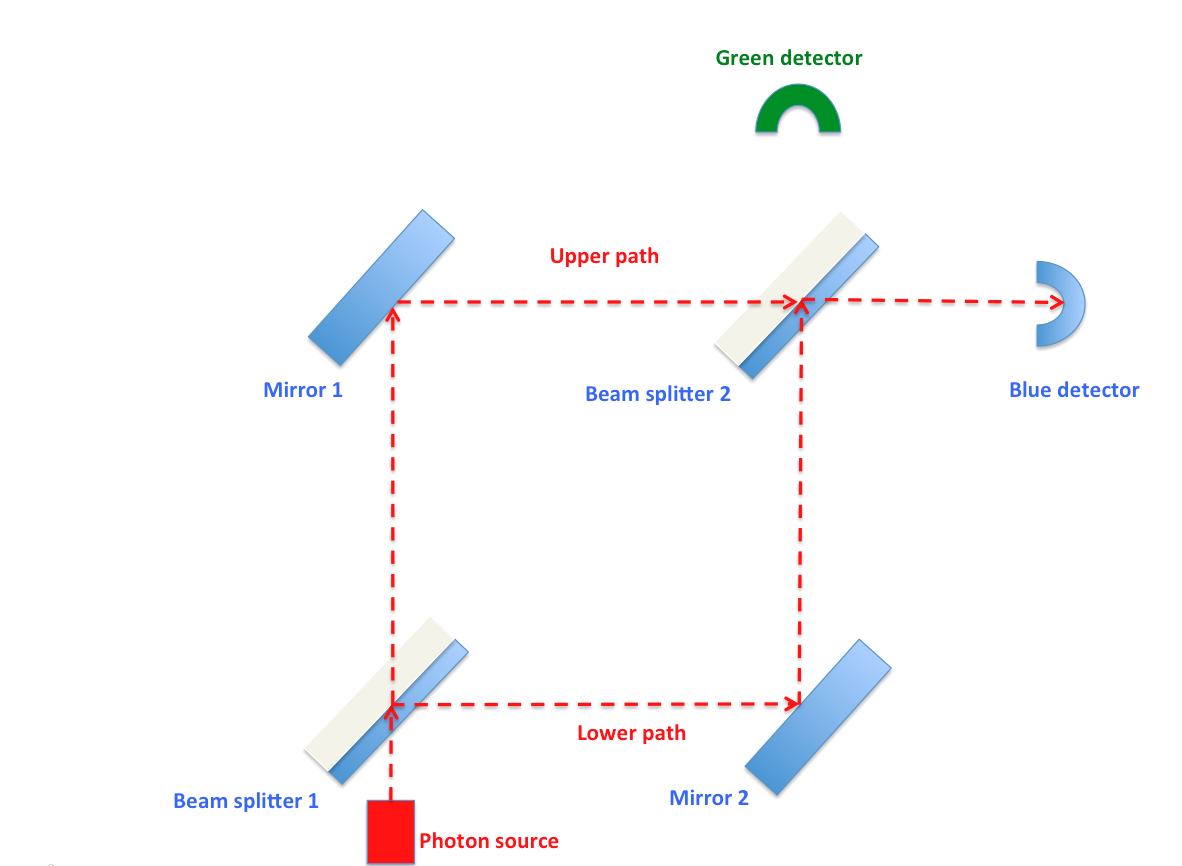
এবার এই কোয়ান্টাম ভাষা মার্খ-জেন্ডার এক্সপেরিমেন্টে প্রয়োগ করা যাক। একটি ফোটন যখন মার্খ-জেন্ডার ইন্টারফেরোমিটারে প্রথম বিম-স্প্লিটারে ওপর আপতিত হয়, তখন সিস্টেমের বেসিস-স্টেট হবে: ।upper> এবং ।lower>;

।upper> প্রতিফলিত ফোটন জন্য এবং ।lower> ট্রান্সমিটেড ফোটনের জন্য। এই বেসিস-স্টেটের সাথে এম্প্লিটিউড যুক্ত করে তাদের যোগফল থেকে আমরা  সিস্টেমের সুপারপজিশন-স্টেট পাবো। আমরা জানি, বিম-স্প্লিটারে ফোটনের প্রতিফলিত কিংবা সরাসরি বেরিয়ে যাওয়ার সম্ভাবনা ৫০%। তাই, প্রথম বিম-স্প্লিটারে সিস্টেমের সুপারপজিশন-স্টেট হবে:

s।upper> + s।lower>

প্রথম বিম-স্প্লিটারে সিস্টেমের সুপারপজিশন-স্টেটের উপাদানগুলোর সেট হলো দ্বিতীয় বিম-স্প্লিটারে সিস্টেমের বেসিস-স্টেট। সুতরাং, দ্বিতীয় বিম-স্প্লিটারে সিস্টেমের বেসিস-স্টেট হলো:  s।upper> এবং s।lower>; নিচে, এই বেসিস-স্টেটের উপাদানদুটির সুপারপজিশন-স্টেটগুলো আলাদা আলাদাভাবে দেখানো হলো। দ্বিতীয় বিম-স্প্লিটারে ওপরে আপতিত ফোটনের ক্ষেত্রে:

s।upper> = s(s।upper> + s।lower>)

দ্বিতীয় বিম-স্প্লিটারে নিচে আপতিত ফোটনের ক্ষেত্রে:

s।lower> = s(s।upper> – s।lower>)

মনে রাখা দরকার, দ্বিতীয় বিম-স্প্লিটারের রুপার প্রলেপে সরাসরি আপতিত ফোটনের প্রতিফলন ইনভার্টেড হয়, তাই ওপরে নেগেটিভ চিহ্নটি এসেছে। যেহেতু প্রথম বিম-স্প্লিটার থেকে দ্বিতীয় বিম-স্প্লিটারে যাবার সময় ফোটনকে পরিমাপ করা হয়নি। তাই, আপডেট-রুল-১ অনুসারে দ্বিতীয় বিম-স্প্লিটারে সিস্টেমের হালনাগাদ হবে। সুতরাং, দ্বিতীয় বিম-স্প্লিটারে সিস্টেমের হালনাগাদকৃত পূর্ণ সুপারপজিশন-স্টেট হবে:

s।upper> + s।lower> = s(s।upper> + s।lower>) + s(s।upper> – s।lower>)

এবার সাধারণ আলজেব্রা ব্যবহার করে:

= s(s।upper> + s।lower>) + s(s।upper> – s।lower>)
= 2s^2।upper>
= ।upper>

অর্থাৎ, আমাদের হিসাব অনুসারে ফোটন যদি প্রথম বিম-স্প্লিটারের ওপরে আপতিত হয়, তবে ফোটনটি সবসময়ই সবুজ ডিটেক্টরে পৌঁছুবে। কোনো ফোটনই নীল ডিটেক্টরে পৌঁছাবে না। বাস্তবে ঠিক এই ব্যাপারটিই ঘটে। একইভাবে যদি প্রথম বিম-স্প্লিটারের নিচে ফোটন আপতিত হয়, তবে ফোটনটি সবসময়ই নীল ডিটেক্টরে পৌঁছুবে।

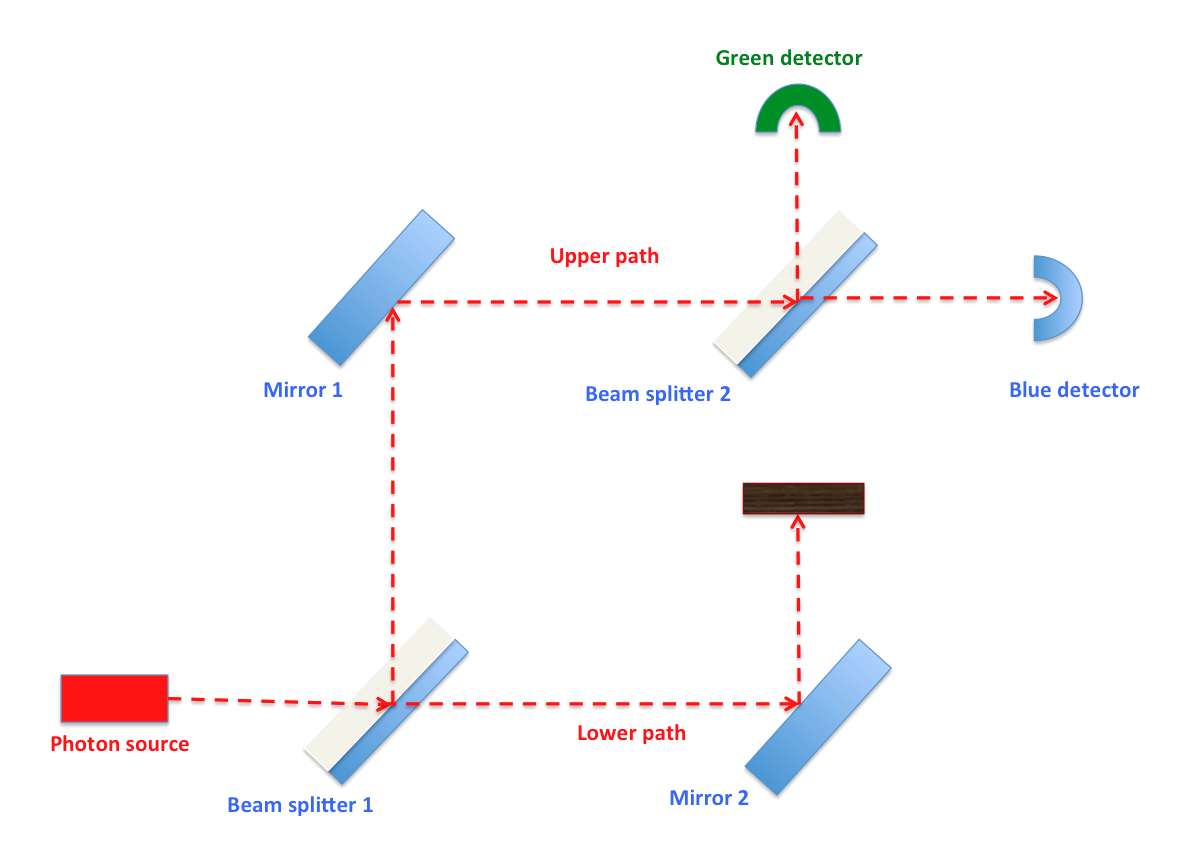
এবার আমরা যদি ওপরের ছবির মতো দ্বিতীয় আয়না এবং দ্বিতীয় বিম-স্প্লিটারের মাঝে একটা প্রতিবন্ধকতা বসাই, তবে এই প্রতিবন্ধকতার উপস্হিতি মূলত পরিমাপকের কাজ করে। ফলে, আমরা আপডেট-রুল-২ এর প্রয়োগ দেখতে পাবো। হিসাব অনুসারে, প্রতিবন্ধকতার উপস্হিতিতে দ্বিতীয় বিম-স্প্লিটারে সিস্টেমের নতুন বেসিস-স্টেট হবে: s।upper> এবং 0; যেহেতু প্রতিবন্ধকতার কারণে নিচের ফোটনটি দ্বিতীয় বিম-স্প্লিটারে পৌঁছুবে না, ফলে s।lower> মান শূন্য। দ্বিতীয় বিম-স্প্লিটারে সিস্টেমের নতুন সুপারপজিশন-স্টেট হবে:

= s(s।upper> + s।lower>)

= s^2।upper> + s^2।lower> 

= 1/2।upper> + 1/2।lower>

অর্থাৎ, দ্বিতীয় বিম-স্প্লিটারে ফোটনগুলোর অর্ধেক অর্ধেক সম্ভাবনা থাকে সবুজ কিংবা নীল ডিটেক্টরে পৌঁছানোর। যথেষ্ট পরিমাণের ফোটন এক্সপেরিমেন্টে ব্যবহার করা হলে আমরা কিছু ফোটনকে সবুজ আর কিছু ফোটনকে নীল ডিটেক্টরে দেখতে পাবো। বাস্তবেও ঠিক এটাই হয়।

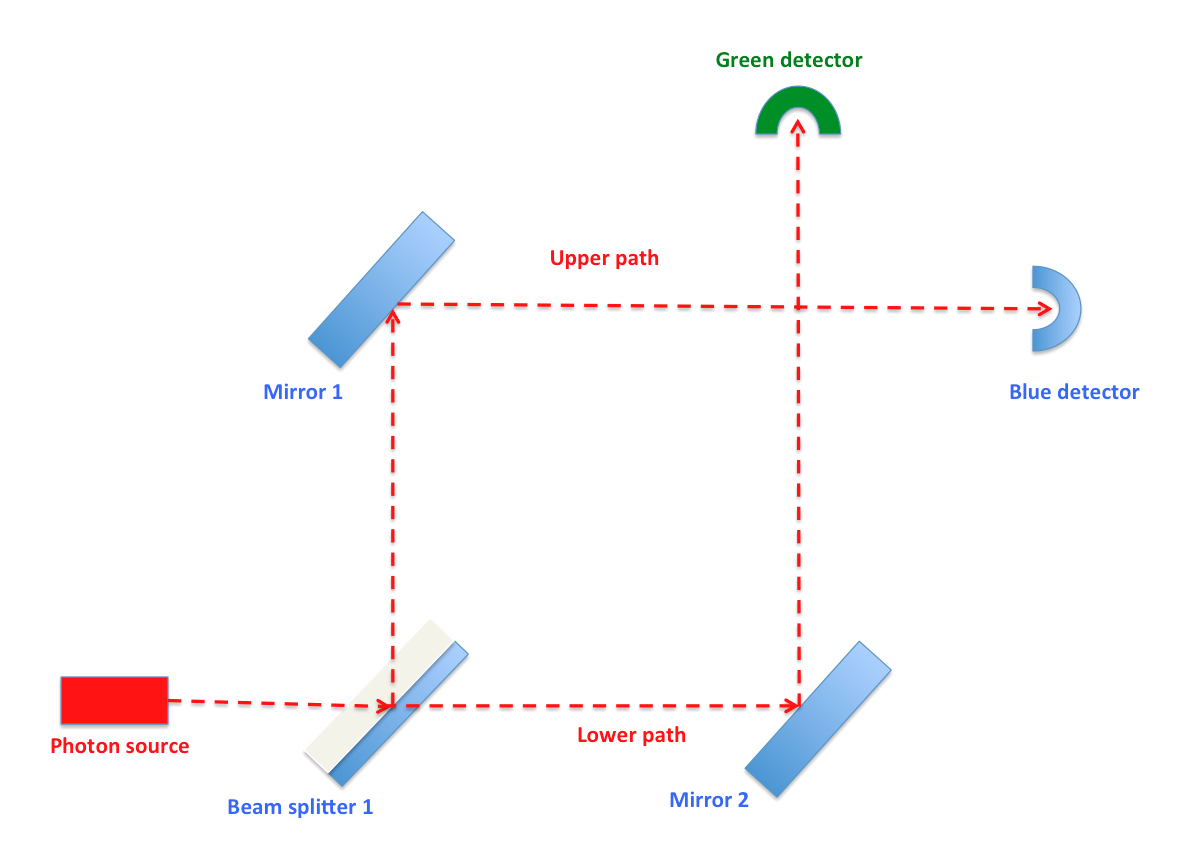
এবার দেখা যাক মার্খ-জেন্ডার এক্সপেরিমেন্টে কম্প্লিমেন্টারিটি-প্রিন্সিপলের প্রভাব। আমরা যদি দ্বিতীয় বিম-স্প্লিটার সরিয়ে নিই, তবে দুটো ডিটেক্টরেই ফোটন পাওয়া সম্ভাবনা হবে ৫০%। অর্থাৎ, মনে হবে যেনো ফোটনেরা কণার মতো আচরণ করছে। আমরা মূলত দ্বিতীয় বিম-স্প্লিটার সরিয়ে নেবার মাধ্যমে এক্সপেরিমেন্টের ইন্টারফেরেন্স বৈশিষ্ট্য অপসারণ করে ফেলেছি। আমরা যদি আবার দ্বিতীয় বিম-স্প্লিটারটি জায়গা মতো বসিয়ে নিই, তবে আমরা এক্সপেরিমেন্টের ইন্টারফেরেন্স ফিরিয়ে আনতে বাধ্য করবো। তখন মনে হবে যেনো, ফোটনেরা তরঙ্গের মতো আচরণ করছে। অর্থাৎ, কোয়ান্টাম-মেকানিক্সে আমাদের পরিমাপই বলে দেয় এক্সপেরিমেন্টের ফলাফল কি হবে। ব্যাপারটা একটু অদ্ভুত বৈকি।

তাহলে, আলো কণা নাকি তরঙ্গ? বস্তুত, কোয়ান্টাম-মেকানিক্সে সবকিছুই কণা। পদার্থ কিংবা শক্তির যে তরঙ্গ রূপ আমরা উপলব্ধি করি, সেটা মূলত কণাদের সম্ভাবনার যোগ-বিয়োগ মাত্র। যেটা মার্খ-জেন্ডার এক্সপেরিমেন্ট থেকে স্পষ্ট হয়ে উঠেছে।

পরের পর্ব: পরিচয় সঙ্কট: বোসন এবং ফার্মিয়ন

অবলম্বনে: “The Great Courses” থেকে প্রকাশিত “Quantum Mechanics: The Physics of the Microscopic World” by “Benjamin Schumacher”